3 The Binomial (and Related) Distributions
3.1 Motivation
Let’s assume we are holding a coin. It may be a fair coin (meaning that the probabilities of observing heads or tails in a given flip of the coin are each 0.5)…or perhaps it is not. We decide that we are going to flip the coin some fixed number of times \(k\), and we will record the outcome of each flip: \[ \mathbf{Y} = \{Y_1,Y_2,\ldots,Y_k\} \,, \] where, e.g., \(Y_1 = 1\) if we observe heads or \(0\) if we observe tails. This is an example of a Bernoulli process, where “process” denotes a sequence of observations, and “Bernoulli” indicates that there are two possible discrete outcomes for each observation.
A binomial experiment is one that generates Bernoulli process data through the running of \(k\) trials (e.g., \(k\) separate coin flips). The properties of such an experiment are that:
- The number of trials \(k\) is fixed in advance.
- Each trial has two possible outcomes, generically denoted as \(S\) (success) or \(F\) (failure).
- The probability of success remains \(p\) throughout the experiment.
- The outcome of any one trial is independent of the outcomes of the others.
The random variable of interest for a binomial experiment is the number of observed successes. A closely related alternative to a binomial experiment is a negative binomial experiment, where the number of successes \(s\) is fixed in advance, instead of the number of trials \(k\), and the random variable of interest is the number of failures that we observe before achieving \(s\) successes. A simple example would be flipping a coin until \(s\) heads are observed and recording the overall number of tails that we observe.
As a side note to the third point above, about the probability of success remaining \(p\) throughout the experiment: binomial and negative binomial experiments rely on sampling with replacement…if we observe a head for a given coin flip, we can observe heads again in the future. In the real world, however, the reader will observe instances where, e.g., a binomial distribution is used to model experiments featuring sampling without replacement: we have \(K = 100\) widgets, of which ten are defective; we check one to see if it is defective (with probability \(p = 0.1\)) and set it aside, then check another (with probability either 10/99 or 9/99, depending on the outcome of the first trial), etc. The convention for using the binomial distribution to model data in such a situation is that it is fine to do so if the number of trials \(k \lesssim K/10\). However, in the age of computers, there is no reason to apply the binomial distribution when we can apply the hypergeometric distribution instead.
And, as a side note to the fourth point above, about the outcome of each trial being independent of the outcomes of the others: in a general process, each datum can be dependent on the data observed previously. How each datum is dependent on previous data defines the type of process that is observed: a Markov process, a Gaussian process, etc. A Bernoulli process is termed a memoryless process because it is comprised of independent (and identically distributed) data.
3.2 Probability Mass Function
Let’s focus first on the outcome of a binomial experiment, with the random variable \(X\) being the number of observed successes in \(k\) trials. What is the probability of observing \(X=x\) successes, if the probability of observing a success in any one trial is \(p\)? \[\begin{align*} \mbox{$x$ successes}&: p^x \\ \mbox{$k-x$ failures}&: (1-p)^{k-x} \,. \end{align*}\] So \(P(X=x) = p^x (1-p)^{k-x}\)…but, no, this isn’t right. Let’s start again and think this through. Assume \(k = 2\). The sample space of possible experimental outcomes is \[ \Omega = \{ SS, SF, FS, FF \} \,. \] If \(p\) = 0.5, then we can see that the probability of observing one success in two trials is 0.5…but our proposed probability mass function tells us that \(P(X=1) = (0.5)^1 (1-0.5)^1 = 0.25\). What are we missing? We are missing that there are two ways of observing a single success…and we need to count both. Because we ultimately do not care about the order in which successes and failures are observed, we utilize counting via combination: \[ \binom{k}{x} = \frac{k!}{x! (k-x)!} \,, \] where the exclamation point represents the factorial function \(x! = x(x-1)(x-2)\cdots 1\). So now we can correctly write down the binomial probability mass function: \[ P(X=x) = p_X(x) = \binom{k}{x} p^x (1-p)^{k-x} ~~~ x \in \{0,\ldots,k\} \,. \] We denote the distribution of the random variable \(X\) as \(X \sim\) Binomial(\(k\),\(p\)). Note that when \(k = 1\), we have a Bernoulli distribution.
Recall: a probability mass function is one way to represent a discrete probability distribution, and it has the properties (a) \(0 \leq p_X(x) \leq 1\) and (b) \(\sum_x p_X(x) = 1\), where the sum is over all values of \(x\) in the distribution’s domain.
(The reader should note that the number of trials is commonly denoted as \(n\), not as \(k\). However, since \(n\) is conventionally used to denote the sample size in an experiment, to avoid confusion we use \(k\) to denote the number of trials in this text.)
In Figure 3.1, we display three binomial pmfs, one each for probabilities of success 0.1 (red, to the left), 0.5 (green, to the center), and 0.8 (blue, to the right). This figure indicates an important aspect of the binomial pmf, namely that it can attain a shape akin to that of a normal distribution, if \(p\) is such that any truncation observed at the values \(x=0\) and \(x=k\) is minimal. In fact, a binomial random variable converges in distribution to a normal random variable in certain limiting situations, as we show in an example below.
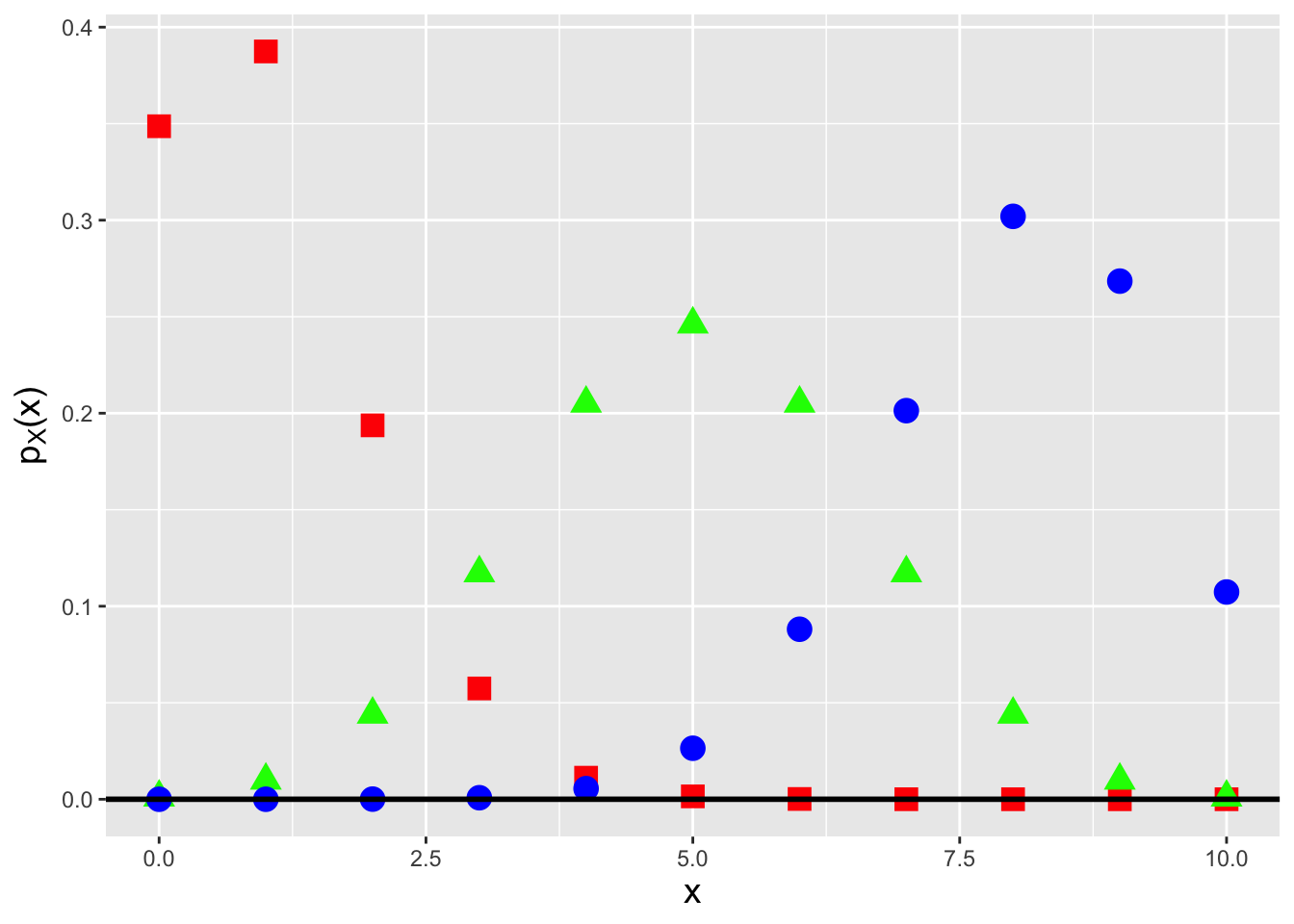
Figure 3.1: Binomial probability mass functions for number of trials \(k = 10\) and success probabilities \(p = 0.1\) (red squares), 0.5 (green triangles), and 0.8 (blue circles).
Recall: the expected value of a discretely distributed random variable is \[ E[X] = \sum_x x p_X(x) \,, \] where the sum is over all values of \(x\) within the domain of the pmf p_X(x). The expected value is equivalent to a weighted average, with the weight for each possible value of \(x\) given by \(p_X(x)\).
For the binomial distribution, the expected value is \[ E[X] = \sum_{x=0}^k x \binom{k}{x} p^x (1-p)^{k-x} \,. \] At first, this does not appear to be easy to evaluate. One trick in our arsenal is to pull constants out of the summation such that whatever is left as the summand is a pmf (and thus sums to 1). Let’s try this here: \[\begin{align*} E[X] &= \sum_{x=0}^k x \binom{k}{x} p^x (1-p)^{k-x} \\ &= \sum_{x=1}^k x \frac{k!}{x!(k-x)!} p^x (1-p)^{k-x} \\ &= \sum_{x=1}^k \frac{k!}{(x-1)!(k-x)!} p^x (1-p)^{k-x} \\ &= kp \sum_{x=1}^k \frac{(k-1)!}{(x-1)!(k-x)!} p^{x-1} (1-p)^{k-x} \,. \end{align*}\] The summation appears almost like that of a binomial random variable. Let’s set \(y = x-1\). Then \[\begin{align*} E[X] &= kp \sum_{x=1}^k \frac{(k-1)!}{(x-1)!(k-x)!} p^{x-1} (1-p)^{k-x} \\ &= kp \sum_{y=0}^{k-1} \frac{(k-1)!}{y!(k-(y+1))!} p^y (1-p)^{k-(y+1)} \\ &= kp \sum_{y=0}^{k-1} \frac{(k-1)!}{y!((k-1)-y)!} p^y (1-p)^{(k-1)-y} \,. \end{align*}\] The summand is now the pmf for the random variable \(Y \sim\) Binomial(\(k-1\),\(p\)), summed over all values of \(y\) in the domain of the distribution. Thus the summation evaluates to 1: \(E[X] = kp\). In an example below, we use a similar strategy to determine the variance \(V[X] = kp(1-p)\).
A negative binomial experiment is governed by the negative binomial distribution, whose pmf is \[ p_X(x) = \binom{x+s-1}{x} p^s (1-p)^x ~~~ x \in \{0,1,\ldots,\infty\} \] The form of this pmf follows from the fact that the underlying Bernoulli process would consist of \(x+s\) data, with the last datum being the observed success that ends the experiment. The first \(x+s-1\) data would feature \(s-1\) successes and \(x\) failures, with the order of success and failure not mattering…so we can view these data as being binomially distributed (albeit with \(x\) representing failures…hence the “negative” in negative binomial!): \[ p_X(x) = \underbrace{\binom{x+s-1}{x} p^{s-1} (1-p)^x}_{\mbox{first $x+s-1$ trials}} \cdot \underbrace{p}_{\mbox{last trial}} \,. \] Note that when \(s = 1\), the resulting distribution is called the geometric distribution.
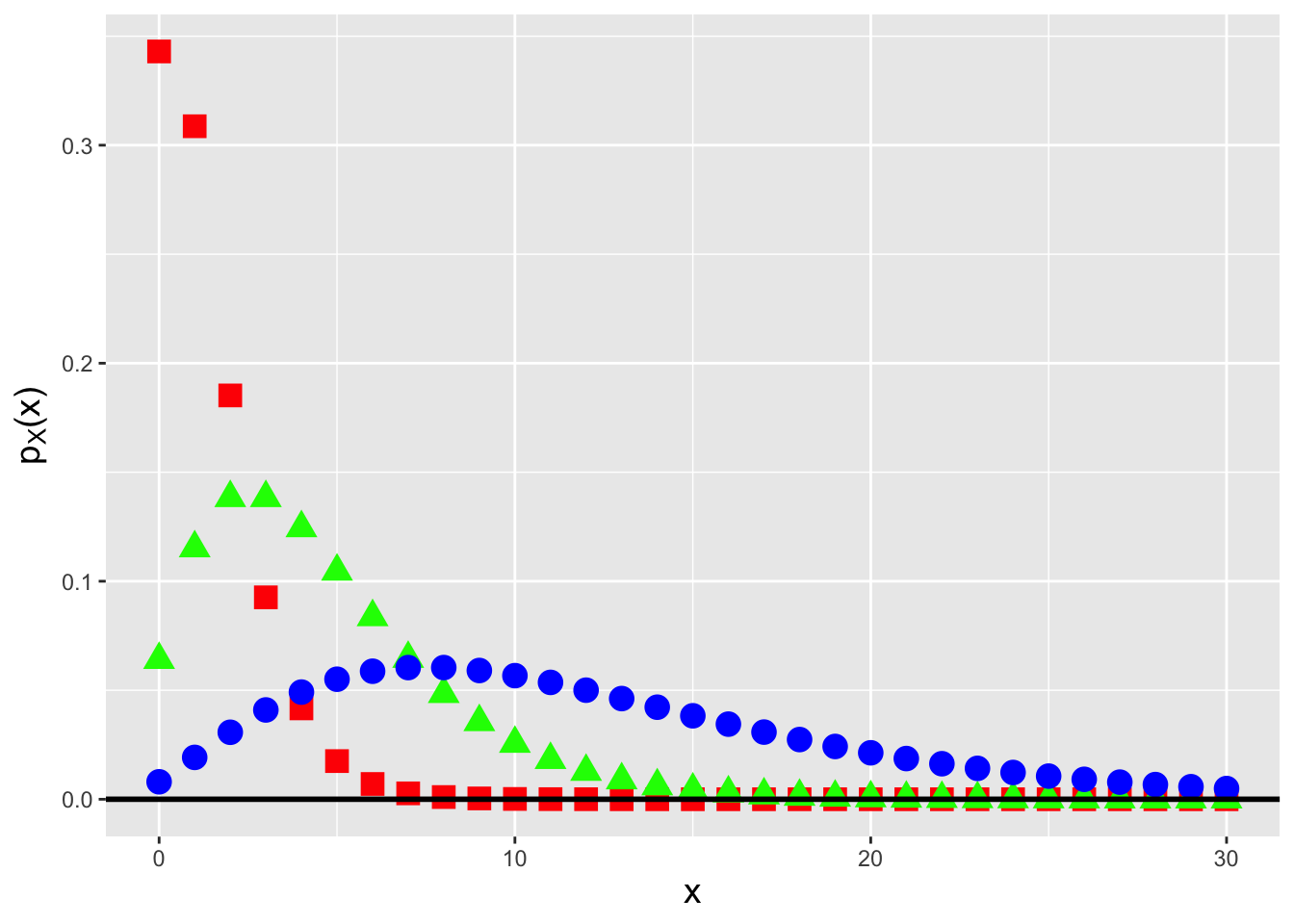
Figure 3.2: Negative binomial probability mass functions for the number of successes \(s = 2\) and success probabilities \(p = 0.7\) (red squares), 0.5 (green triangles), and 0.2 (blue circles).
In an example below, we show how one would derive the expected value of a negative binomial random variable, \(E[X] = s(1-p)/p\). (We can enact a similar calculation to show that the variance is \(V[X] = s(1-p)/p^2\).)
3.2.1 Variance of a Binomial Random Variable
Recall: the variance of a discretely distributed random variable is \[ V[X] = \sum_x (x-\mu)^2 p_X(x) = E[X^2] - (E[X])^2\,, \] where the sum is over all values of \(x\) in the domain of the pmf \(p_X(x)\). The variance represents the square of the “width” of a probability mass function, where by “width” we mean the range of values of \(x\) for which \(p_X(x)\) is effectively non-zero.
The variance of a random variable is given by the shortcut formula that we have been using since Chapter 1: \(V[X] = E[X^2] - (E[X])^2\). So we would expect that we would need to compute \(E[X^2]\) here, since we already know that \(E[X] = kp\). But for reasons that will become apparent below, it is actually far easier for us to compute \(E[X(X-1)]\), and to work with that to eventually derive the variance: \[\begin{align*} E[X(X-1)] &= \sum_{x=0}^k x(x-1) \binom{k}{x} p^x (1-p)^{k-x} \\ &= \sum_{x=0}^k x(x-1) \frac{k!}{x!(k-x)!} p^x (1-p)^{k-x} \\ &= \sum_{x=2}^k \frac{k!}{(x-2)!(k-x)!} p^x (1-p)^{k-x} \\ &= k(k-1) p^2 \sum_{x=2}^k \frac{(k-2)!}{(x-2)!(k-x)!} p^{x-2} (1-p)^{k-x} \,. \end{align*}\] The advantage to using \(x(x-1)\) was that it matches the first two terms of \(x! = x(x-1)\cdots(1)\), allowing easy cancellation. If we set \(y = x-2\), we find that the summand above will, in a similar manner as in the calculation of \(E[X]\), become the pmf for the random variable \(Y \sim\) Binomial(\(k-2,p\))…and thus the summation will evaluate to 1.
So \(E[X(X-1)] = E[X^2] - E[X] = k(k-1)p^2\), and \(E[X^2] = k^2p^2-kp^2 + kp = V[X] + (E[X])^2\), and \(V[X] = k^2p^2-kp^2+kp-k^2p^2 = kp-kp^2 = kp(1-p)\). Done.
3.2.2 The Expected Value of a Negative Binomial Random Variable
The calculation for the expected value \(E[X]\) for a negative binomial random variable is similar to that for a binomial random variable: \[\begin{align*} E[X] &= \sum_{x=0}^{\infty} x \binom{x+s-1}{x} p^s (1-p)^x \\ &= \sum_{x=0}^{\infty} x \frac{(x+s-1)!}{(s-1)!x!} p^s (1-p)^x \\ &= \sum_{x=1}^{\infty} \frac{(x+s-1)!}{(s-1)!(x-1)!} p^s (1-p)^x \,. \end{align*}\] Let \(y = x-1\). Then \[\begin{align*} E[X] &= \sum_{y=0}^{\infty} \frac{(y+s)!}{(s-1)!y!} p^s (1-p)^{y+1} \\ &= \sum_{y=0}^{\infty} s(1-p) \frac{(y+s)!}{s!y!} p^s (1-p)^y \\ &= \sum_{y=0}^{\infty} \frac{s(1-p)}{p} \frac{(y+s)!}{s!y!} p^{s+1} (1-p)^y \\ &= \frac{s(1-p)}{p} \sum_{y=0}^{\infty} \frac{(y+s)!}{s!y!} p^{s+1} (1-p)^y \\ &= \frac{s(1-p)}{p} \,. \end{align*}\] The summand is that of a negative binomial distribution for \(s+1\) successes, hence the summation is 1, and thus \(E[X] = s(1-p)/p\).
We can use a similar calculation in which we evaluate \(E[X(X-1)]\) in order to derive the variance of a negative binomial random variable: \(V[X] = s(1-p)/p^2\).
3.2.3 Binomial Distribution: Normal Approximation
In certain limiting situations, a binomial random variable converges in distribution to a normal random variable. In other words, if \[ P\left(\frac{X-\mu}{\sigma} < a \right) = P\left(\frac{X-kp}{\sqrt{kp(1-p)}} < a \right) \approx P(Z < a) = \Phi(a) \,, \] then we can state that \(X \stackrel{d}{\rightarrow} Y \sim \mathcal{N}(kp,kp(1-p))\), or that \(X\) converges in distribution to a normal random variable \(Y\). Now, what do we mean by “certain limiting situations”? For instance, if \(p\) is close to zero or one, then the binomial distribution is truncated at 0 or at \(k\), and the shape of the pmf does not appear to be like that of a normal pdf. One convention is that the normal approximation is adequate if \[ k > 9\left(\frac{\mbox{max}(p,1-p)}{\mbox{min}(p,1-p)}\right) \,. \] The reader might question why we would mention this approximation at all: if we have binomially distributed data and a computer, then we need not ever utilize such an approximation to, e.g., compute probabilities. This point is correct (and is the reason why, for instance, we do not mention the so-called continuity correction here; our goal is not to compute probabilities). The reason we mention this is that this approximation underlies a commonly used hypothesis test framework, the Wald interval, that we will mention later in the chapter.
3.2.4 Computing Probabilities
Let \(X\) be a random variable sampled from a binomial distribution with number of trials \(k = 6\) and success probability \(p = 0.4\), and let \(Y\) be a random variable sampled from a negative binomial distribution with number of successes \(s = 3\) and success probability \(p = 0.6\).
- What is \(P(2 \leq X < 4)\)?
To find this probability, we sum over the binomial probability mass function for values \(x = 2\) and \(x = 3\). (The form of the inequalities matter for discrete distributions!) We can perform this computation analytically: \[\begin{align*} P(2 \leq X < 4) &= \binom{6}{2} (0.4)^2 (1-0.4)^4 + \binom{6}{3} (0.4)^3 (1-0.4)^3 \\ &= \frac{6!}{2!4!} \cdot 0.16 \cdot 0.1296 + \frac{6!}{3!3!} \cdot 0.064 \cdot 0.216 = 15 \cdot 0.0207 + 20 \cdot 0.0138 = 0.5875 \,. \end{align*}\] There is a 58.75% chance that the next time we sample data according to this distribution, we will observe a value of 2 or 3.
It is ultimately simpler to use
Rto perform this calculation. While we can compute the probability as the difference of two cumulative distribution function values, for discrete distributions it is often more straightforward to sum over the relevant probability masses directly, since then we need not worry about whether the input to the cdf is correct given the form of the inequality:
## [1] 0.58752
- What is \(P(Y > 1)\)?
If we were to determine this probability by hand, the first thing we would do is specify that we will compute \(1 - P(Y \leq 3)\), as this has a finite (and small!) number of terms: \[\begin{align*} P(Y > 1) &= 1 - \binom{0+3-1}{0} (0.6)^3 (1-0.6)^0 - \binom{1+3-1}{1} (0.6)^3 (1-0.6)^1 \\ &= 1 - 1 \cdot 0.216 \cdot 1 - 3 \cdot 0.216 \cdot 0.4 = 0.5248 \,. \end{align*}\] There is a 52.48% chance that we would observe more than one failure the next time we sample data according to this distribution.
Like before, it is ultimately simpler to use
R:
## [1] 0.52483.2.5 The Binomial Distribution as Part of the Exponential Family
Recall that the exponential family of distributions, introduced in the last chapter, comprises distributions whose probability mass or density functions can be written in the form \[\begin{align*} h(x) \exp\left( \eta(\theta)T(x) - A(\theta) \right) \,. \end{align*}\] Is the binomial distribution a member of the larger exponential family of distributions? It would initially appear that the answer is no (as there are no exponential functions in its pmf), but if we note that \[\begin{align*} p^x = \exp\left(\log p^x\right) = \exp\left(x \log p\right) \end{align*}\] and that \[\begin{align*} (1-p)^{k-x} = \exp\left(\log (1-p)^{k-x}\right) = \exp\left((k-x) \log (1-p)\right) \,, \end{align*}\] we can see that \[\begin{align*} p_X(x \vert p) = \binom{k}{x} \exp\left( x [ \log(p) - \log(1-p) ] + k \log (1-p) \right) \end{align*}\] and thus that \[\begin{align*} h(x) &= \binom{k}{x} \\ \eta(p) &= \log(p) - \log(1-p) = \log \frac{p}{1-p} \\ T(x) &= x \\ A(p) &= -k \log(1-p) \,. \end{align*}\] The binomial distribution is indeed a member of the exponential family. We will leave it as an exercise to the reader to show that the negative binomial distribution lies within the exponential family as well.
3.3 Cumulative Distribution Function
Recall: the cumulative distribution function, or cdf, is another means by which to encapsulate information about a probability distribution. For a discrete distribution, it is defined as \(F_X(x) = \sum_{y\leq x} p_Y(y)\), and it is defined for all values \(x \in (-\infty,\infty)\), with \(F_X(-\infty) = 0\) and \(F_X(\infty) = 1\).
For the binomial distribution, the cdf is \[ F_X(x) = \sum_{y=0}^{\lfloor x \rfloor} p_Y(y) = \sum_{y=0}^{\lfloor x \rfloor} \binom{k}{y} p^y (1-p)^{k-y} \,, \] where \(\lfloor x \rfloor\) denotes the floor function, which returns the largest integer that is less than or equal to \(x\) (e.g., if \(x\) = 6.75, \(\lfloor x \rfloor\) = 6). (In closed form, we can represent this cdf with a regularized incomplete beta function, which is not analytically easy to work with.) Also, because a pmf is defined at discrete values of \(x\), its associated cdf is a step function, as illustrated in the left panel of Figure 3.3. As we can see in this figure, the cdf steps up at each value of \(x\) in the domain of \(p_X(x)\), and unlike the case for continuous distributions, the form of the inequalities in a probabilistic statement matter: \(P(X < x)\) and \(P(X \leq x)\) will not be the same, if \(x\) is an integer with value \(\{0,1,2,\ldots,k\}\).
Recall: an inverse cdf function \(x = F_X^{-1}(q)\) takes as input a distribution quantile \(q \in [0,1]\) and returns the value of \(x\). A discrete distribution has no unique inverse cdf; it is convention to utilize the generalized inverse cdf, \(x = \mbox{inf}\{x : F_X(x) \geq q\}\), where “inf” indicates that the function is to return the smallest value of \(x\) such that \(F_X(x) \geq q\).
In the right panel of Figure 3.3, we display the inverse cdf for the same distribution used to generate the figure in the left panel (\(k=4\) and \(p=0.5\)). Like the cdf, the inverse cdf for a discrete distribution is a step function. Below, in an example, we show how we adapt the inverse transform sampler algorithm of Chapter 1 to accommodate the step-function nature of an inverse cdf.
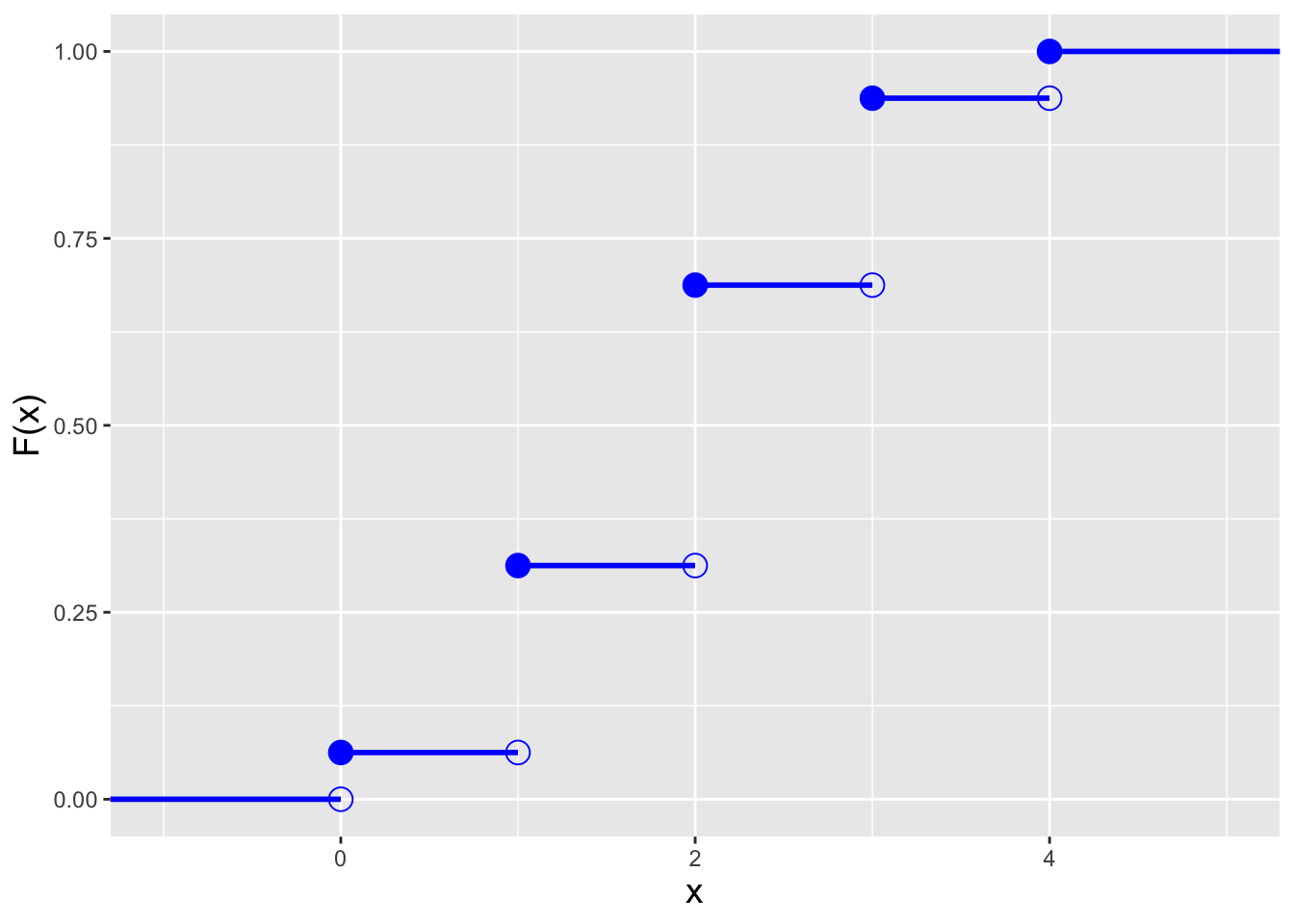
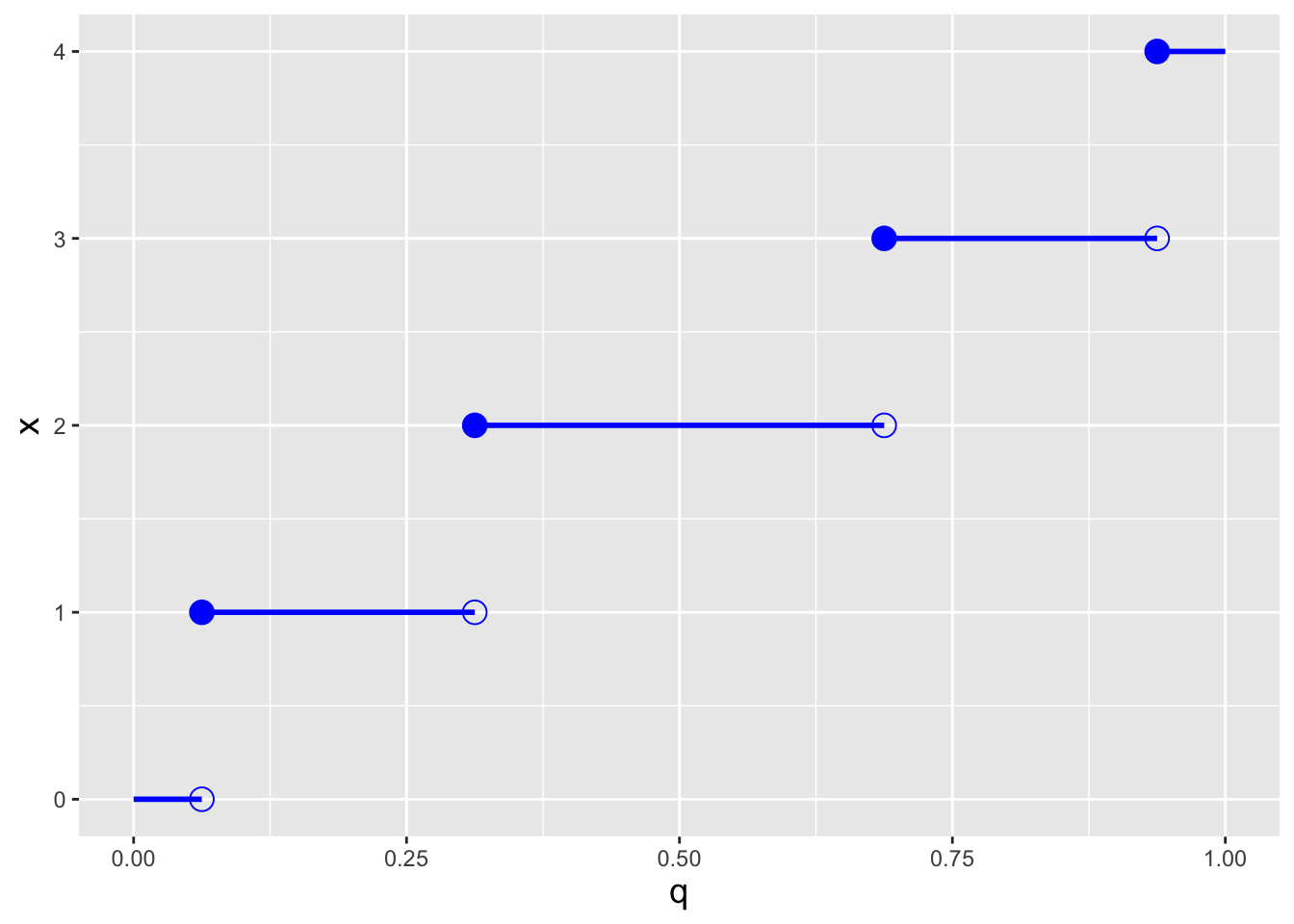
Figure 3.3: Illustration of the cumulative distribution function \(F_X(x)\) (left) and inverse cumulative distribution function \(F_X^{-1}(q)\) (right) for a binomial distribution with number of trials \(k = 4\) and probability of success \(p=0.5\).
3.3.1 Computing Probabilities
Because computing the binomial pmf for a range of values of \(x\) can be laborious, we typically utilize
Rfunctions when computing probabilities.
- If \(X \sim\) Binomial(10,0.6), which is \(P(4 \leq X < 6)\)?
We first note that due to the form of the inequality, we do not include \(X=6\) in the computation. Thus \(P(4 \leq X < 6) = p_X(4) + p_X(5)\), which equals \[ \binom{10}{4} (0.6)^4 (1-0.6)^6 + \binom{10}{5} (0.6)^5 (1-0.6)^5 \,. \] Even computing this is unnecessarily laborious; instead, we call on
R:
## [1] 0.3121349(This utilizes
R’s vectorization feature: we need not explicitly define afor-loop to evaluatedbinom()for \(x=4\) and then at \(x=5\).) We can also utilize cdf functions here: \(P(4 \leq X < 6) = P(X < 6) - P(X < 4) = P(X \leq 5) - P(X \leq 3) = F_X(5) - F_X(3)\), which inRis computed via
## [1] 0.3121349As we can see, the direct summation approach is the more straightforward one.
- \(X \sim\) Binomial(10,0.6), what is the value of \(a\) such that \(P(X \leq a) = 0.9\)?
First, we set up the inverse cdf formula: \[ P(X \leq a) = F_X(a) = 0.9 ~~ \Rightarrow ~~ a = F_X^{-1}(0.9) \] Note that we didn’t do anything differently here than we would have done in a continuous distribution setting…and we can proceed directly to
Rbecause it utilizes the generalized inverse cdf algorithm.
## [1] 8We can see immediately how the cdf for a discrete distribution is not a one-to-one function, as if we plug \(x = 8\) into the cdf, we will not recover the initial value \(q = 0.9\):
## [1] 0.95364263.3.2 Sampling Data From an Arbitrary Probability Mass Function
While we would always utilize
Rshortcut functions likerbinom()when they exist, there may be instances when we need to code our own functions for sampling data from discrete distributions. The code below shows such a function for an arbitrary probability mass function.
set.seed(101)
x <- c(1,2,4,8) # domain of x
p.x <- c(0.2,0.35,0.15,0.3) # p_X(x)
F.x <- cumsum(p.x) # cumulative sum -> produces F_X(x)
n <- 100
q <- runif(n) # we still ultimately need runif!
i <- findInterval(q,F.x)+1 # the output are bin numbers [0,3], and not [1,4]
# hence we add 1
# 1 means q is between 0 and F.x[1], etc.
x.sample <- x[i]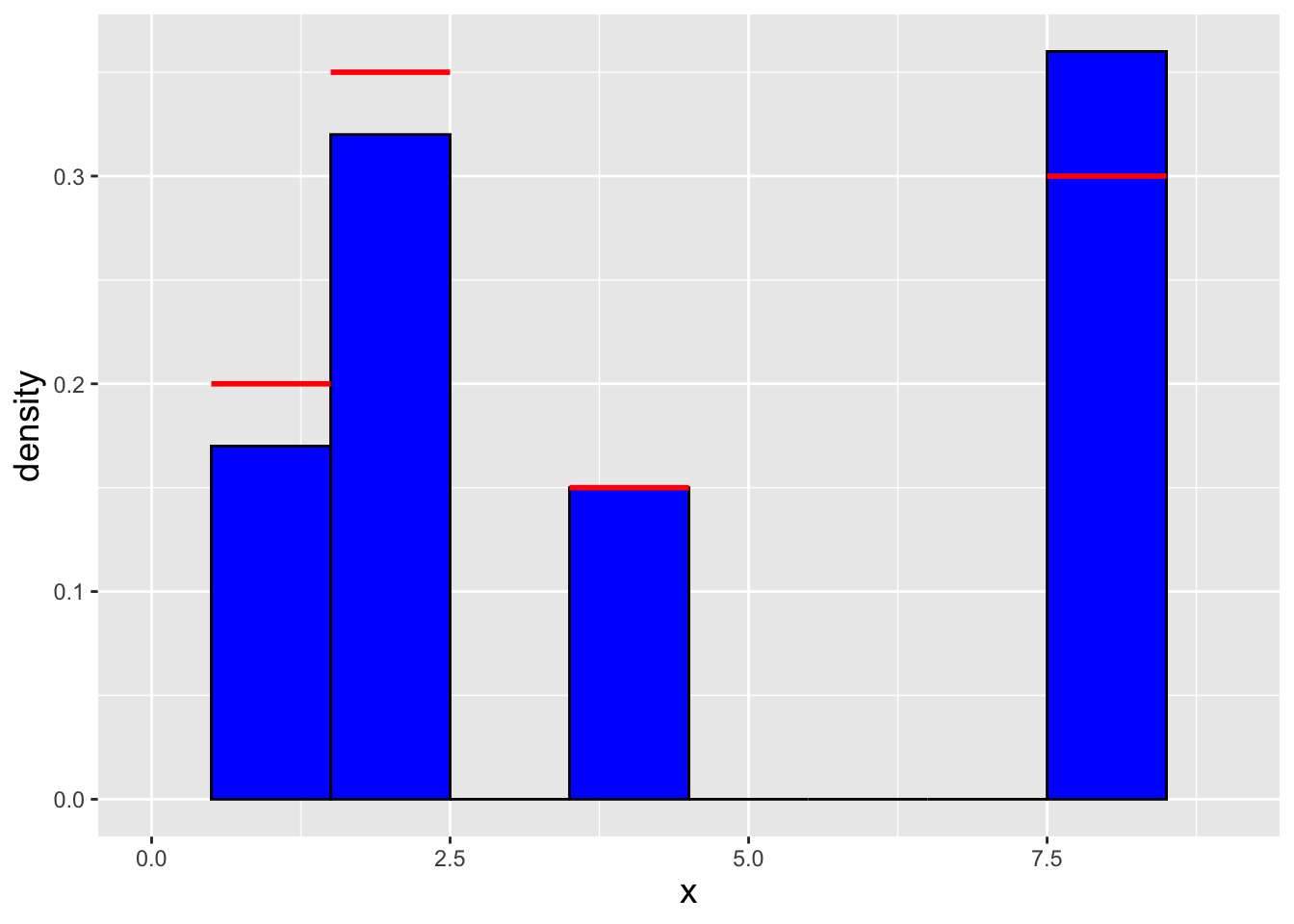
Figure 3.4: Histogram of \(n = 100\) iid data drawn using an inverse tranform sampler adapted to the discrete distribution setting. The red lines indicate the true density for each value of \(x\).
3.4 Linear Functions of Random Variables
Let’s assume we are given \(n\) iid binomial random variables: \(X_1,X_2,\ldots,X_n \sim\) Binomial(\(k\),\(p\)). Can we determine the distribution of the sum \(Y = \sum_{i=1}^n X_i\)? Yes, we can…via the method of moment-generating functions.
Recall: the moment-generating function, or mgf, is a means by which to encapsulate information about a probability distribution. When it exists, the mgf is given by \(m_X(t) = E[e^{tX}]\). Also, if \(Y = \sum_{i=1}^n a_iX_i\), then \(m_Y(t) = m_{X_1}(a_1t) m_{X_2}(a_2t) \cdots m_{X_n}(a_nt)\); if we can identify \(m_Y(t)\) as the mgf for a known family of distributions, then we can immediately identify the distribution for \(Y\) and the parameters of that distribution.
The mgf for the binomial distribution is \[\begin{align*} m_X(t) = E[e^{tX}] &= \sum_{x=0}^k e^{tx} \binom{k}{x} p^x (1-p)^{k-x} \\ &= \sum_{x=0}^k \binom{k}{x} (pe^t)^x (1-p)^{k-x} \,. \end{align*}\] We utilize the binomial theorem \[ (x+y)^k = \sum_{i=0}^k \binom{k}{i} x^i y^{k-i} \] to re-express \(m_X(t)\): \[ m_X(t) = [pe^t + (1-p)]^k \,. \] Note that one may see this written as \((pe^t+q)^k\), where \(q = 1-p\).
The mgf for \(Y = \sum_{i=1}^n X_i\) is thus \[ m_Y(t) = \prod_{i=1}^n m_{X_i}(t) = [m_X(t)]^n = [pe^t + (1-p)]^{nk} \,. \] We can see that this has the form of a binomial mgf: \(Y \sim\) Binomial(\(nk\),\(p\)), with expected value \(E[Y] = nkp\) and variance \(V[Y] = nkp(1-p)\). This makes sense, as the act of summing binomial data is equivalent to concatenating \(n\) separate Bernoulli processes into one longer Bernoulli process…whose data can subsequently be modeled using a binomial distribution.
While we can identify the distribution of the sum by name, we cannot
say the same about the sample mean.
We know that the expected value is \(E[\bar{X}] = \mu = kp\)
and that the variance is \(V[\bar{X}] = \sigma^2/n = kp(1-p)/n\),
but when we attempt to use the mgf method with
\(a_i = 1/n\) instead of \(a_i = 1\), we find that
\[
m_{\bar{X}}(t) = [pe^{t/n} + (1-p)]^{nk} \,.
\]
Changing \(t\) to \(t/n\) has the effect of creating an mgf that does not
have the form of any known mgf.
However, we do know the distribution: it has a pmf that is identical
in form to that of the binomial distribution, but has the domain
\(\{0,1/n,2/n,...,k\}\).
(We can derive this result mathematically by making
the transformation \(\sum_{i=1}^n X_i \rightarrow (\sum_{i=1}^n X_i)/n\),
as we see below in an example.)
We could define the pmf ourselves
using our own R function, but there is no real need to: as we will see,
if we wish to construct a confidence interval for \(p\), we can just use the sum
\(\sum_{i=1}^n X_i\) as our statistic.
(We could also, in theory, utilize the Central Limit Theorem if
\(n \gtrsim 30\), but there is absolutely no reason to do that to make
inferences about \(p\): we know the distribution of the sum of the data
exactly, and thus there is no need to fall back upon approximations.)
3.4.1 The MGF for a Geometric Random Variable
Recall that a geometric distribution is equivalent to a negative binomial distribution with number of successes \(s = 1\); its probability mass function is \[ p_X(x) = p (1-p)^x \,, \] with \(x = \{0,1,\ldots\}\) and \(p \in [0,1]\). The moment-generating function for a geometric random variable is thus \[\begin{align*} m_X(t) = E[e^{tX}] &= \sum_{x=0}^{\infty} e^{tx} p (1-p)^x = p \sum_{x=0}^\infty e^{tx} (1-p)^x \\ &= p \sum_{x=0}^\infty [e^t(1-p)]^x = \frac{p}{1-e^t(1-p)} \,. \end{align*}\] The last equality utilizes the formula for the sum of an infinite geometric series: \(\sum_{i=0}^\infty x^i = (1-x)^{-1}\), when \(\vert x \vert < 1\). (If \(t < 0\) and \(p > 0\), then the condition that \(\vert e^t(1-p) \vert < 1\) holds.)
The sum of \(s\) geometric random variables has the moment-generating function \[ m_Y(t) = \prod_{i=1}^s m_{X_i}(t) = \left[\frac{p}{1-e^t(1-p)}\right]^s \,. \] This is the mgf for a negative binomial distribution for \(s\) successes. In the same way that the sum of \(k\) Bernoulli random variables is a binomially distributed random variable, the sum of \(s\) geometric random variables is a negative binomially distributed random variable.
3.4.2 The PMF for the Sample Mean
Let’s assume we are given \(n\) iid binomial random variables: \(X_1,X_2,\ldots,X_n \sim\) Binomial(\(k\),\(p\)). As we observe above, the distribution of the sum \(Y = \sum_{i=1}^k X_i\) is binomial with mean \(nkp\) and variance \(nkp(1-p)\).
The sample mean is \(\bar{X} = Y/n\), and so \[ F_{\bar{X}}(\bar{x}) = P(\bar{X} \leq \bar{x}) = P(Y \leq n\bar{x}) = \sum_{y=0}^{n\bar{x}} p_Y(y) \,. \] (We note that \(n\bar{x}\) is integer-valued by definition; we do not need to round down here.) Because we are dealing with a pmf, we cannot simply take the derivative of \(F_{\bar{X}}(\bar{x})\) to find \(f_{\bar{X}}(\bar{x})\)…but what we can do is assess the jump in the cumulative distribution function at each step, because that is the pmf. In other words, we can compute \[ f_{\bar{X}}(\bar{x}) = P(Y \leq n\bar{x}) - P(Y \leq n\bar{x}-1) \] and store this as a numerically expressed pmf for \(\bar{X}\). See Figure 3.5.
But it turns out we can say more about this pmf, by looking at the problem in a different way. We know that \(Y \sim\) Binomial\((nkp,nkp(1-p))\) and thus that \(Y \in [0,1,\ldots,nk]\). When we compute the quotient \(\bar{X} = Y/n\), all we are doing is redefining the domain of the pmf from being \([0,1,\ldots,nk]\) to being \([0,1/n,2/n,\ldots,k]\). We do not actually change the probability masses! So we can write \[ p_{\bar{X}}(\bar{x}) = \binom{nk}{n\bar{x}} p^{n\bar{x}} (1-p)^{nk-n\bar{x}} ~~ \bar{x} \in [0,1/n,2/n,\ldots,k] \,. \] This pmf has the functional form of a binomial pmf…but not the domain of a binomial pmf. For that reason, we cannot say that \(\bar{X}\) is binomially distributed. The pmf has a functional form, it has a domain, but it has no known “name” and thus no associated
Rfunctions that we can utilize when performing statistical inference. (This is why we will utilize the sum of the data instead:Rfunctions for its distribution exist!)
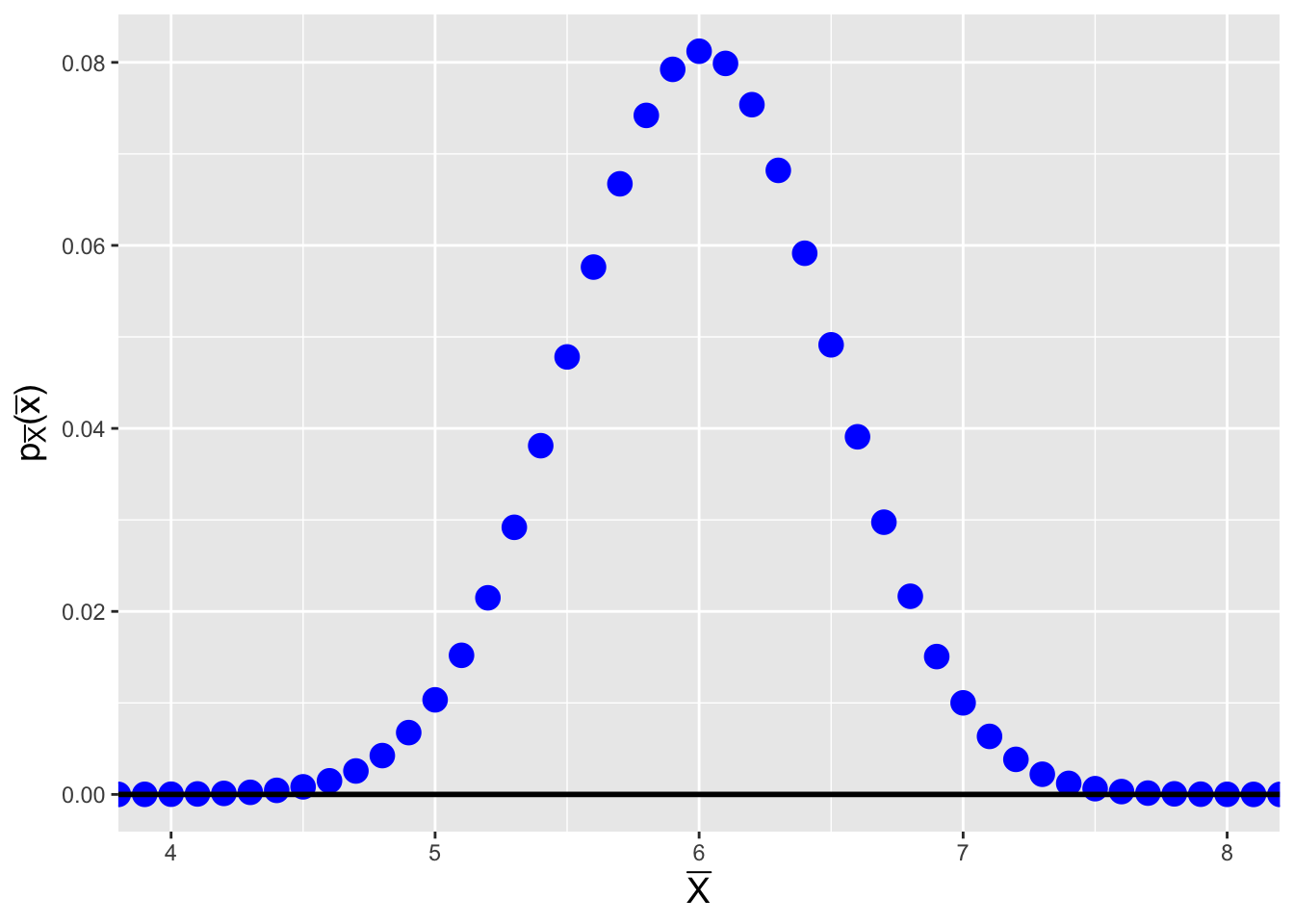
Figure 3.5: Probability mass function for the sample mean of \(n = 10\) iid binomial random variables, for \(k = 10\) and \(p = 0.6\).
3.5 Order Statistics
Let’s suppose that we have sampled \(n\) iid random variables \(\{X_1,\ldots,X_n\}\) from some arbitrary distribution. Previously, we have summarized such data with the sample mean and the sample variance. However, there are other summary statistics, some of which are only calculable if we sort the data into ascending order: \(\{X_{(1)},\ldots,X_{(n)}\}\). These are dubbed order statistics and the \(j^{th}\) order statistic is the sample’s \(j^{th}\) smallest value (i.e., the smallest-valued datum in the sample is \(X_{(1)}\) and the largest-valued datum is \(X_{(n)}\)). Examples of statistics based on ordering include \[\begin{align*} \mbox{Range:}& ~~X_{(n)} - X_{(1)} \\ \mbox{Median:}& ~~X_{(n+1)/2} ~ \mbox{if $n$ is odd} \\ & ~~(X_{n/2}+X_{(n+1)/2})/2 ~ \mbox{if $n$ is even} \,. \end{align*}\] The most important point to keep in mind is that the probability mass and density functions for order statistics differ from the pmfs and pdfs for their constituent iid data. For instance, if we sample \(n\) data from a \(\mathcal{N}(0,1)\) distribution, we would not expect the minimum value to be distributed the same way; if anything, the mean should take on larger and larger negative values, and the variance on those values should decrease, as \(n\) increases.
So: why are we discussing order statistics here, in the middle of a discussion of the binomial distribution? It is because we can derive, e.g., the pdf for an order statistic of a continuous distribution using the binomial pmf. (Note that order statistics exist for discretely valued data, but the probability mass functions for them are not easily derived and thus we will only consider order statistics for continuously valued data here.)
![\label{fig:order}If we have, e.g., a probability density function $f_X(x)$ whose domain is $[a,b]$, and we view success as sampling a datum less than a given value $x$, then when we sample $n$ data, the number that have values $\leq x$ is a binomial random variable with $k=n$ and $p = F_X(x)$.](figures/order.png)
Figure 3.6: If we have, e.g., a probability density function \(f_X(x)\) whose domain is \([a,b]\), and we view success as sampling a datum less than a given value \(x\), then when we sample \(n\) data, the number that have values \(\leq x\) is a binomial random variable with \(k=n\) and \(p = F_X(x)\).
See Figure 3.6. Without loss of generality, we can assume that \(f_X(x) > 0\) for \(x \in [a,b]\) and that we sample \(n\) data from this distribution. The number of data \(X\) that have value less than some arbitrarily chosen \(x\) is a binomial random variable: \[ Y \sim \mbox{Binomial}(n,p=F_X(x)) \] What is the probability that the \(j^{th}\) ordered datum has a value \(\leq x\)? That’s equivalent to asking for the probability that \(Y \geq j\), i.e., did we see at least \(j\) successes in \(n\) trials? \[ F_{(j)}(x) = P(X_{(j)} \leq x) = P(Y \geq j) = \sum_{i=j}^n \binom{n}{i} [F_X(x)]^i [1 - F_X(x)]^{n-i} \,. \] \(F_{(j)}(x)\) is the cdf for the \(j^{th}\) ordered datum.
Recall: a continuous distribution’s pdf is the derivative of its cdf.
Leaving aside algebraic details, we can write down the pdf for \(X_{(j)}\): \[ f_{(j)}(x) = \frac{d}{dx}F_{(j)}(x) = \frac{n!}{(j-1)!(n-j)!} f_X(x) [F_X(x)]^{j-1} [1 - F_X(x)]^{n-j} \,, \] and write down simplified expressions for the pdfs for the minimum and maximum data values: \[ f_{(1)}(x) = n f_X(x) [1 - F_X(x)]^{n-1} ~~\mbox{and}~~ f_{(n)}(x) = n f_X(x) [F_X(x)]^{n-1} \,. \]
3.5.1 Distribution of the Minimum Value Sampled from an Exponential Distribution
The probability density function for an exponential random variable is \[ f_X(x) = \frac{1}{\theta} \exp\left(-\frac{x}{\theta}\right) \,, \] for \(x \geq 0\) and \(\theta > 0\), and the expected value of \(X\) is \(E[X] = \theta\). What is the pdf for the smallest value among \(n\) iid data sampled from an exponential distribution? What is the expected value for the smallest value?
First, if we do not immediately recall the cumulative distribution function \(F_X(x)\), we can easily derive it: \[ F_X(x) = \int_0^x \frac{1}{\theta} e^{-y/\theta} dy = 1 - e^{-x/\theta} \,. \] We plug \(F_X(x)\) into the expression of the pdf of the minimum datum given above: \[\begin{align*} f_{(1)}(x) &= n \frac{1}{\theta} e^{-x/\theta} \left[ 1 - (1-e^{-x/\theta}) \right]^{n-1} \\ &= n \frac{1}{\theta} e^{-x/\theta} e^{-(n-1)x/\theta} \\ &= \frac{n}{\theta} e^{-nx/\theta} \,. \end{align*}\] \(X_{(1)}\) is thus an exponentially distributed random variable with parameter \(\theta/n\) and expected value \(\theta/n\). We can derive this result as follows. \[ E[X_{(1)}] = \int_0^\infty x \frac{n}{\theta} e^{-nx/\theta} dx \,. \] We recognize this as almost having the form of a gamma-function integral: \[ \Gamma(u) = \int_0^\infty x^{u-1} e^{-x} dx \,. \] We affect a variable transformation \(y = nx/\theta\); for this transformation, \(dy = (n/\theta)dx\), and if \(x = 0\) or \(\infty\), \(y = 0\) or \(\infty\) (meaning the integral bounds are unchanged). Our new integral is \[ E[X] = \int_0^\infty \frac{\theta y}{n} \frac{n}{\theta} e^{-y} \frac{\theta}{n} dy = \frac{\theta}{n} \int_0^\infty y e^{-y} dy = \frac{\theta}{n} \Gamma(2) = \frac{\theta}{n} 1! = \frac{\theta}{n} = \frac{E[X]}{n} \,. \]
3.5.2 Distribution of the Median Value Sampled from a Uniform(0,1) Distribution
The probability density function for a Uniform(0,1) distribution is \[ f_X(x) = 1 \] for \(x \in [0,1]\). The cdf for this distribution is thus \[ F_X(x) = \int_0^x 1 dy = x \,. \] Let’s assume that we sample \(n\) iid data from this distribution, where \(n\) is an odd number. The index of the median value is thus \((n+1)/2\), and if we plug into the general expression for the pdf of the \(m^{th}\) ordered datum, we find that \[\begin{align*} f_{(n+1)/2} &= \frac{n!}{\left(\frac{n+1}{2}-1\right)!\left(n - \frac{n+1}{2}\right)!} \cdot 1 \cdot x^{\left(\frac{n+1}{2}\right)-1} \cdot (1-x)^{n - \left(\frac{n+1}{2}\right)} \\ &= \frac{n!}{2\left(\frac{n-1}{2}\right)!} x^{\left(\frac{n-1}{2}\right)} (1-x)^{\left(\frac{n-1}{2}\right)} \,. \end{align*}\] As we will see later, this is a beta distribution with parameters \(\alpha = \beta = (n+1)/2\). The median value has expected value 1/2 and a variance that shrinks with \(n\).
3.6 Point Estimation
In the first two chapters, we introduce a number of concepts related to point estimation, the act of using statistics to make inferences about a population parameter \(\theta\). We…
- assess point estimators using the metrics of bias, variance, mean-squared error, and consistency;
- utilize the Fisher information metric to determine the lower bound on the variance for unbiased estimators (the Cramer-Rao Lower Bound, or CRLB); and
- define estimators via the maximum likelihood algorithm, which generates estimators that are at least asymptotically unbiased and at least asymptotically reach the CRLB, and which converge in distribution to normal random variables.
We will review these concepts in the context of estimating population quantities for binomial distributions below, in the body of the text and in examples. For now…
Recall: the bias of an estimator is the difference between the average value of the estimates it generates and the true parameter value. If \(E[\hat{\theta}-\theta] = 0\), then the estimator \(\hat{\theta}\) is said to be unbiased.
Recall: the value of \(\theta\) that maximizes the likelihood function is the maximum likelihood estimate, or MLE, for \(\theta\). The maximum is found by taking the (partial) derivative of the (log-)likelihood function with respect to \(\theta\), setting the result to zero, and solving for \(\theta\). That solution is the maximum likelihood estimate \(\hat{\theta}_{MLE}\). Also recall the invariance property of the MLE: if \(\hat{\theta}_{MLE}\) is the MLE for \(\theta\), then \(g(\hat{\theta}_{MLE})\) is the MLE for \(g(\theta)\).
Here we will introduce another means by which to define an estimator. The minimum variance unbiased estimator (or MVUE) is the one that has the smallest variance among all unbiased estimators of \(\theta\). The reader’s first thought might be “well, why didn’t we use this estimator in the first place…after all, the MLE is not guaranteed to yield an unbiased estimator, so why have we put off discussing the MVUE?” The primary reasons are that MVUEs are sometimes not definable (i.e., we can reach insurmountable roadblocks when trying to derive them), and unlike MLEs, they do not exhibit the invariance property. (For instance, if \(\hat{\theta}_{MLE} = \bar{X}\), then \(\hat{\theta^2}_{MLE} = \bar{X}^2\), but if \(\hat{\theta}_{MVUE} = \bar{X}\), it is not necessarily the case that \(\hat{\theta^2}_{MVUE} = \bar{X}^2\).) However, we should always at least try to define the MVUE, because if we can, it will be at least equal the performance of, if not do better than, the MLE, in terms of bias and/or variance.
There are two steps to carry out when deriving the MVUE:
- determining a sufficient statistic for \(\theta\); and
- correcting any bias that is observed when we utilize that sufficient statistic as our initial estimator.
A sufficient statistic for a parameter \(\theta\) captures all information about \(\theta\) contained in the sample. The sufficiency principle holds that if, e.g., \(Y\) is a sufficient statistic for \(\theta\), and we collect two datasets \(\mathbf{U}\) and \(\mathbf{V}\) such that \(Y(\mathbf{U}) = Y(\mathbf{V})\), then the inferences we make about \(\theta\) given that we observe \(\mathbf{U}\) will be exactly the same as those we would make if we were to observe \(\mathbf{V}\) instead. Using any statistic beyond a sufficient statistic will not lead to improved inferences about \(\theta\). This means that, for instance, combining \(\bar{X}\) (a sufficient statistic for the normal mean \(\mu\) when the variance is known) with, say, the sample median will not reduce the length of confidence intervals for \(\mu\) or change the power of hypothesis tests about \(\mu\), relative to what we would derive using \(\bar{X}\) alone. Note that utilizing the sufficiency principle is but one way by which statisticians can attempt data reduction prior to inference; two others, which are beyond the scope of this book, are the likelihood and equivalence principles. For a deeper treatment of sufficiency and of data reduction than we provide here, the interested reader should consult Chapter 6 of Casella and Berger (2002).
A statistic \(Y(\mathbf{X})\) is a sufficient statistic for \(\theta\) if the ratio \[\begin{align*} \frac{f_X(\mathbf{x} \vert \theta)}{f_Y(y \vert \theta)} \mathrel{{iid}\rightarrow} \frac{\prod_{i=1}^n f_X(x_i \vert \theta)}{f_Y(y \vert \theta)} \,, \end{align*}\] where \(f_Y(y \vert \theta)\) is the probability density function of the sampling distribution for \(Y\), is constant as a function of \(\theta\). We note that by this definition, \(\mathbf{X}\) itself comprises a sufficient statistic for \(\theta\), as does the full set of order statistics \(\{X_{(1)},\ldots,X_{(n)}\}\). The relevant questions are: can we define a sufficient statistic that actually reduces the data? and if so, how can we identify it?
Let’s answer the second question first. The simplest way by which to identify a sufficient statistic is to write down the likelihood function and then to factorize it into two separate functions, one of which depends only on the observed data and the other of which depends on both the observed data and the parameter of interest: \[ \mathcal{L}(\theta \vert \mathbf{x}) = g(\mathbf{x},\theta) \cdot h(\mathbf{x}) \,. \] This is the so-called factorization criterion. In the expression \(g(\mathbf{x},\theta)\), the data will appear within, e.g., a summation (e.g., \(\sum_{i=1}^n x_i\)) or a product (e.g., \(\prod_{i=1}^n x_i\)), and we would identify that summation or product as a sufficient statistic for \(\theta\). For instance, for the binomial distribution, the factorized likelihood (given \(n\) iid data) is \[ \mathcal{L}(p \vert \mathbf{x}) = \prod_{i=1}^n \binom{k}{x_i} p^{x_i} (1-p)^{k-x_i} = \underbrace{\left[ \prod_{i=1}^n \binom{k}{x_i} \right]}_{h(\mathbf{x})} \underbrace{p^{\sum_{i=1}^n x_i} (1-p)^{nk-\sum_{i=1}^n x_i}}_{g(\sum_{i=1}^n x_i,p)} \,. \] By inspecting the function \(g(\mathbf{x},p)\), we immediately determine that a sufficient statistic for \(p\) is \(Y = \sum_{i=1}^n X_i\). We say “a” sufficient statistic because sufficient statistics are not unique: any one-to-one function of a sufficient statistic is also a sufficient statistic. For instance, if \(Y = \sum_{i=1}^n X_i\) is a sufficient statistic for \(\theta\), so is \(Y = \bar{X}\), etc.
Now we return to the first question above: can we define a sufficient statistic that actually reduces the data? The answer is “not always.” In fact, across all possible distributions, it is relatively rare that we can do this. The Pitman-Koopman-Darmois theorem holds that, among families of distributions that do not have domain-specifying parameters, only the exponential family of distributions have sufficient statistics whose dimension does not increase as the sample size increases. (This theorem motivates, in large part, our introduction of the exponential family in Chapter 2.) Recall that the exponential family of distributions comprises a set of distributions whose probability mass or density functions can be written as \[\begin{align*} h(x) \exp\left( \eta(\theta) T(x) - A(\theta) \right) \,. \end{align*}\] (Here we assume that the distribution has just one free parameter \(\theta\).) In this expression, \(T(x)\) is the sufficient statistic; as seen in a previous example, for the binomial distribution \(T(X) = X\). If we collect \(n\) iid data, then the sufficient statistic is \(T(\mathbf{X}) = \sum_{i=1}^n X_i\), and as we can see it is still a single number\(-\)i.e., it has a dimension of one\(-\)regardless of the value of \(n\). Now, restricting ourselves to exponential family distributions in inferential situations would appear to limit the practical utility of the sufficiency principle…except it is the case that many (if not most) of the distributions that we utilize in inference are indeed exponential-family distributions, including all the ones that we focus on in this book.
(We note here for completeness that once we identify a sufficient statistic, we are technically required to demonstrate that it is both minimally sufficient and complete, as it needs to be both so that we can use it, e.g., to determine the minimum variance unbiased estimator. It suffices to say here that the sufficient statistics that we identify for exponential family distributions via likelihood factorization are minimally sufficient and complete. See Chapter 7 for more details on minimal sufficiency and completeness.)
If \(Y\) is a sufficient statistic for \(\theta\), and there is a function \(h(Y)\) that is an unbiased estimator for \(\theta\) and that depends on the data only through \(Y\), then \(h(Y)\) is the MVUE for \(\theta\). (Recall from above that one-to-one functions of sufficient statistics are themselves sufficient statistics, hence \(h(Y)\) is sufficient for \(\theta\).) Here, given \(Y = \sum_{i=1}^n X_i\), we need to find a function \(h(\cdot)\) such that \(E[h(Y)] = p\). Earlier in this chapter, we determined that the distribution for the sum of iid binomial random variables is Binomial(\(nk\),\(p\)), and thus we know that this distribution has expected value \(nkp\). Thus \[ E\left[Y\right] = nkp ~\implies~ E\left[\frac{Y}{nk}\right] = p ~\implies~ h(Y) = \frac{Y}{nk} = \frac{\bar{X}}{k} ~\mbox{is the MVUE for}~p \,. \] The variance of \(\hat{p}\) is \[ V[\hat{p}] = V\left[\frac{\bar{X}}{k}\right] = \frac{1}{k^2}V[\bar{X}] = \frac{1}{k^2} \frac{V[X]}{n} = \frac{1}{k^2}\frac{kp(1-p)}{n} = \frac{p(1-p)}{nk} \,. \] We know that this variance abides by the restriction \[ V[\hat{p}] \geq \frac{1}{nI(p)} = -\frac{1}{nE\left[\frac{d^2}{dp^2} \log p_X(X \vert p) \right]} \,. \] But is it equivalent to the lower bound for unbiased estimators, the CRLB? (Note that in particular situations, the MVUE may have a variance larger than the CRLB; when this is the case, unbiased estimators that achieve the CRLB simply do not exist.) For the binomial distribution, \[\begin{align*} p_{X}(x) &= \binom{k}{x} p^{x} (1-p)^{k-x} \\ \log p_{X}(x) &= \log \binom{k}{x} + x \log p + (k-x) \log (1-p) \\ \frac{d}{dp} \log p_{X}(x) &= 0 + \frac{x}{p} - \frac{k-x}{(1-p)} \\ \frac{d^2}{dp^2} \log p_{X}(x) &= -\frac{x}{p^2} - \frac{k-x}{(1-p)^2} \\ E\left[\frac{d^2}{dp^2} \log p_{X}(X)\right] &= -\frac{1}{p^2}E[X] - \frac{1}{(1-p)^2}E[k-X] \\ &= -\frac{kp}{p^2}-\frac{k-kp}{(1-p)^2} \\ &= -\frac{k}{p}-\frac{k}{1-p} = -\frac{k}{p(1-p)} \,. \end{align*}\] The lower bound on the variance is thus \(p(1-p)/(nk)\), and so the MVUE does achieve the CRLB. We cannot define a better unbiased estimator for \(p\) than \(\bar{X}/k\).
3.6.1 The MLE for the Binomial Success Probability
Recall: the value of \(\theta\) that maximizes the likelihood function is the maximum likelihood estimate, or MLE, for \(\theta\). The maximum is found by taking the (partial) derivative of the (log-)likelihood function with respect to \(\theta\), setting the result to zero, and solving for \(\theta\). That solution is the maximum likelihood estimate \(\hat{\theta}_{MLE}\).
Above, we determined that the likelihood function for \(n\) iid binomial random variables \(\{X_1,\ldots,X_n\}\) is \[ \mathcal{L}(p \vert \mathbf{x}) = \left[\prod_{i=1}^n \binom{k}{x_i} \right] p^{\sum_{i=1}^n x_i} (1-p)^{nk-\sum_{i=1}^n x_i} \,. \] Recall that the value \(\hat{p}_{MLE}\) that maximizes \(\mathcal{L}(p \vert x)\) also maximizes \(\ell(p \vert x) = \log \mathcal{L}(p \vert x)\), which is considerably easier to work with: \[\begin{align*} \ell(p \vert \mathbf{x}) &= \left(\sum_{i=1}^n x_i\right) \log p + \left(nk - \sum_{i=1}^n x_i\right) \log (1-p) \\ \frac{d}{dp} \ell(p \vert \mathbf{x}) &= \frac{1}{p} \sum_{i=1}^n x_i - \frac{1}{1-p} \left(nk - \sum_{i=1}^n x_i\right) = 0 \,. \end{align*}\] (Here, we drop the binomial coefficient, which does not depend on \(p\) and thus differentiates to zero.) After rearranging terms, we find that \[ p = \frac{1}{nk}\sum_{i=1}^n x_i ~\implies~ \hat{p}_{MLE} = \frac{\bar{X}}{k} \,. \] The MLE matches the MVUE, thus we know that the MLE is unbiased and we know that it achieves the CRLB.
A useful property of MLEs is the invariance property, whereby the MLE for a function of \(\theta\) is given by applying the same function to the MLE itself. Thus
- the MLE for the population mean \(E[X] = \mu = kp\) is \(\hat{\mu}_{MLE} = \bar{X}\); and
- the MLE for the population variance \(V[X] = \sigma^2 = kp(1-p)\) is \(\widehat{\sigma^2}_{MLE} = \bar{X}(1-\bar{X}/k)\).
Last, note that asymptotically, \(\hat{p}_{MLE}\) converges in distribution to a normal random variable: \[ \hat{p}_{MLE} \stackrel{d}{\rightarrow} Y \sim \mathcal{N}\left(p,\frac{1}{nI(p)} = \frac{p(1-p)}{nk}\right) \,. \]
3.6.2 Sufficient Statistics for the Normal Distribution
If we have \(n\) iid data drawn from a normal distribution with unknown mean \(\mu\) and unknown variance \(\sigma^2\), then the factorized likelihood is \[ \mathcal{L}(\mu,\sigma^2 \vert \mathbf{x}) = \underbrace{(2 \pi \sigma^2)^{-n/2} \exp\left(-\frac{1}{2\sigma^2}\sum_{i=1}^n x_i^2\right)\exp\left(\frac{\mu}{\sigma^2}\sum_{i=1}^n x_i\right)\exp\left(-\frac{n\mu^2}{2\sigma^2}\right)}_{g(\sum x_i^2, \sum x_i,\mu,\sigma)} \cdot \underbrace{1}_{h(\mathbf{x})} \,. \] Here, we identify \(\sum x_i^2\) and \(\sum x_i\) as joint sufficient statistics: we need two pieces of information to jointly estimate \(\mu\) and \(\sigma^2\). (To be clear: it is not necessarily the case that one of the parameters matches up to one of the statistics…rather, the two statistics are jointly sufficient for estimation.) We thus cannot proceed further to define an MVUE for \(\mu\) or for \(\sigma^2\), without knowing the joint bivariate probability density function for \(Y_1 = \sum_{i=1}^n X_i^2\) and \(Y_2 = \sum_{i=1}^n X_i\).
(Note that we can proceed if we happen to know either \(\mu\) or \(\sigma^2\); if one of these values is fixed, then there will only be one sufficient statistic and we can determine the MVUE for the other, freely varying parameter.)
3.6.3 The Sufficiency Principle: Examples of When We Cannot Reduce Data
As stated above, it is often impossible to reduce data to, e.g., a single-number summary. The following examples, utilizing distributions that are not exponential-family distributions, illustrate this.
- A Laplace distribution with scale parameter 1 has the probability density function \[\begin{align*} f_X(x \vert \theta) &= \frac12 e^{-\vert x - \theta \vert} \,, \end{align*}\] where \(x \in (-\infty,\infty)\) and \(\theta \in (-\infty,\infty)\). If we observe \(n\) iid data, then likelihood factorization yields \[\begin{align*} \mathcal{L}(\theta \vert \mathbf{x}) = \frac{1}{2^n} e^{-\sum_{i=1}^n \vert x_i - \theta \vert} \,. \end{align*}\] \(Y = \sum_{i=1}^n \vert X_i - \theta \vert\) is not a sufficient statistic as it contains the (unknown) parameter: a sufficient statistic for \(\theta\) cannot contain \(\theta\) itself! We cannot isolate a function of \(\mathbf{X}\) alone, and thus no data reduction is possible.
- A Cauchy distribution with scale parameter 1 has the probability density function \[\begin{align*} f_X(x \vert \theta) = \frac{1}{\pi (x-\theta)^2} \,, \end{align*}\] where \(x \in (-\infty,\infty)\) and \(\theta \in (-\infty,\infty)\). If we observe \(n\) iid data, then likelihood factorization yields \[\begin{align*} \mathcal{L}(\theta \vert \mathbf{x}) = \frac{1}{\pi^n} \frac{1}{\prod_{i=1}^n (x_i-\theta)^2} \,. \end{align*}\] Again, we cannot isolate a function of the \(X_i\)’s alone: no data reduction is possible.
3.6.4 The MVUE for the Exponential Mean
The exponential distribution is \[ f_X(x) = \frac{1}{\theta} \exp\left(-\frac{x}{\theta}\right) \,, \] where \(x \geq 0\) and \(\theta > 0\), and where \(E[X] = \theta\) and \(V[X] = \theta^2\). Let’s assume that we have \(n\) iid data drawn from this distribution. Can we define the MVUE for \(\theta\)? For \(\theta^2\)?
The likelihood function is \[ \mathcal{L}(\theta \vert \mathbf{x}) = \prod_{i=1}^n f_X(x_i \vert \theta) = \frac{1}{\theta^n}\exp\left(-\frac{1}{\theta}\sum_{i=1}^n x_i \right) = h(\mathbf{x}) \cdot g(\theta,\mathbf{x}) \,. \] Here, there are no terms that are functions of only the data, so \(h(\mathbf{x}) = 1\) and a sufficient statistic is \(Y = \sum_{i=1}^n X_i\). We compute the expected value of \(Y\): \[ E[Y] = E\left[\sum_{i=1}^n X_i\right] = \sum_{i=1}^n E[X_i] = \sum_{i=1}^n \theta = n\theta \,. \] The expected value of \(Y\) is not \(\theta\), so \(Y\) is not unbiased…but we can see immediately that \(E[Y/n] = \theta\), so that \(Y/n\) is unbiased. Thus the MVUE for \(\theta\) is thus \(\hat{\theta}_{MVUE} = Y/n = \bar{X}\).
Note that the MVUE does not possess the invariance property…it is not necessarily the case that \(\hat{\theta^2}_{MVUE} = \bar{X}^2\).
Let’s propose a function of \(Y\) and see if we can use that to define \(\hat{\theta^2}_{MVUE}\): \(h(Y) = Y^2/n^2 = \bar{X}^2\). (To be clear, we are simply proposing a function and seeing if it helps us define what we are looking for. It might not. If not, we can try again with another function of \(Y\).) Utilizing what we know about the sample mean, we can write down that \[ E[\bar{X}^2] = V[\bar{X}] + (E[\bar{X}])^2 = \frac{V[X]}{n} + (E[X])^2 = \frac{\theta^2}{n}+\theta^2 = \theta^2\left(\frac{1}{n} + 1\right) \,. \] So \(\bar{X}^2\) itself is not an unbiased estimator of \(\theta^2\)…but we can see that \(\bar{X}^2/(1/n+1)\) is. Hence \[ \hat{\theta^2}_{MVUE} = \frac{\bar{X}^2}{\left(\frac{1}{n}+1\right)} \,. \]
3.6.5 The MVUE for the Geometric Distribution
Recall that the geometric distribution is a negative binomial distribution with \(s = 1\): \[\begin{align*} p_X(x) = \binom{x + s - 1}{x} p^s (1-p)^x ~ \rightarrow ~ p(1-p)^x \,, \end{align*}\] where \(p \in (0,1]\) and where \(E[X] = (1-p)/p\) and \(V[X] = (1-p)/p^2\). Let’s assume that we sample \(n\) iid data from this distribution. Can we define the MVUE for \(p\)? For \(1/p\)?
The likelihood function is \[\begin{align*} \mathcal{L}(p \vert \mathbf{x}) = \prod_{i=1}^n p_X(x_i \vert p) = p^n (1-p)^{\sum_{i=1}^n x_i} = 1 \cdot g(p,\mathbf{x}) \,. \end{align*}\] We identify a sufficient statistic as \(Y = \sum_{i=1}^n X_i\); the expected value of \(Y\) is \[\begin{align*} E[Y] = E\left[\sum_{i=1}^n X_i\right] = \sum_{i=1}^n E[X_i] = \sum_{i=1}^n \frac{1-p}{p} = n\left(\frac{1}{p}-1\right) \,. \end{align*}\] We cannot “debias” this expression to find the MVUE for \(p\): \[\begin{align*} E\left[\frac{Y}{n}+1\right] = \frac{1}{p} \,. \end{align*}\] Specifically, \[\begin{align*} E\left[\frac{1}{Y/n+1}\right] \neq 1/E\left[\frac{Y}{n}+1\right] = p \,. \end{align*}\] However, we did determine the MVUE for \(1/p\): \(Y/n+1 = \bar{X}+1\). But as there is no invariance property for the MVUE, we cannot use this expression to write down an MVUE for \(p\).
3.7 Confidence Intervals
Recall: a confidence interval is a random interval \([\hat{\theta}_L,\hat{\theta}_U]\) that overlaps (or covers) the true value \(\theta\) with probability \[ P\left( \hat{\theta}_L \leq \theta \leq \hat{\theta}_U \right) = 1 - \alpha \,, \] where \(1 - \alpha\) is the confidence coefficient. We determine \(\hat{\theta}\) by solving the following equation: \[ F_Y(y_{\rm obs} \vert \theta) - q = 0 \,, \] where \(F_Y(\cdot)\) is the cumulative distribution function for the statistic \(Y\), \(y_{\rm obs}\) is the observed value of the statistic, and \(q\) is an appropriate quantile value that is determined using the confidence interval reference table introduced in section 16 of Chapter 1.
A concept that we have not explicitly discussed up until now is the “duality” between confidence intervals and hypothesis tests: as they are mathematically related, one can, in theory, “invert” hypothesis tests to derive confidence intervals and vice-versa. We illustrate this duality in Figure 3.7, in which we assume that the distribution from which we are to sample data is a normal distribution with mean \(\mu\) and known variance \(\sigma^2\). The parallel green lines in the figure represent lower and upper rejection region boundaries as a function of (the null hypothesis value) \(\mu\). Let’s say that we pick a specific value of \(\mu\), say \(\mu = \mu_o = 1\), and draw a vertical line at that coordinate. The part of that line that lies between the parallel green lines (indicated in solid red) indicates the range of observed statistic values \(y_{\rm obs}\) for which we would fail to reject the null, and the parts above and below the parallel lines (shown in dashed red) would indicate \(y_{\rm obs}\) values for which we would reject the null. (These are the acceptance and rejection regions, respectively; “acceptance region” is a term that we have not used up until now, but it simply denotes the range of statistic values for which we would fail to reject a null hypothesis, when it is indeed correct.) Confidence intervals, on the other hand, are ranges of values of \(\mu\) for which a given value of \(y_{\rm obs}\) lies in the acceptance region. (For instance, the dashed horizontal blue line in the figure shows the range of values associated with a two-sided confidence interval for \(\mu\) given \(y_{\rm obs} = 0.5\).) We can see that for a given value of \(\mu\), if we were to sample a value of \(y_{\rm obs}\) between the two green lines (with probability \(1-\alpha\)), then the associated confidence interval will overlap \(\mu\), and if we sample a value of \(y_{\rm obs}\) outside the green lines (with probability \(\alpha\)), the confidence interval will not overlap \(\mu\). The confidence interval coverage is thus exactly \(100(1-\alpha)\) percent.
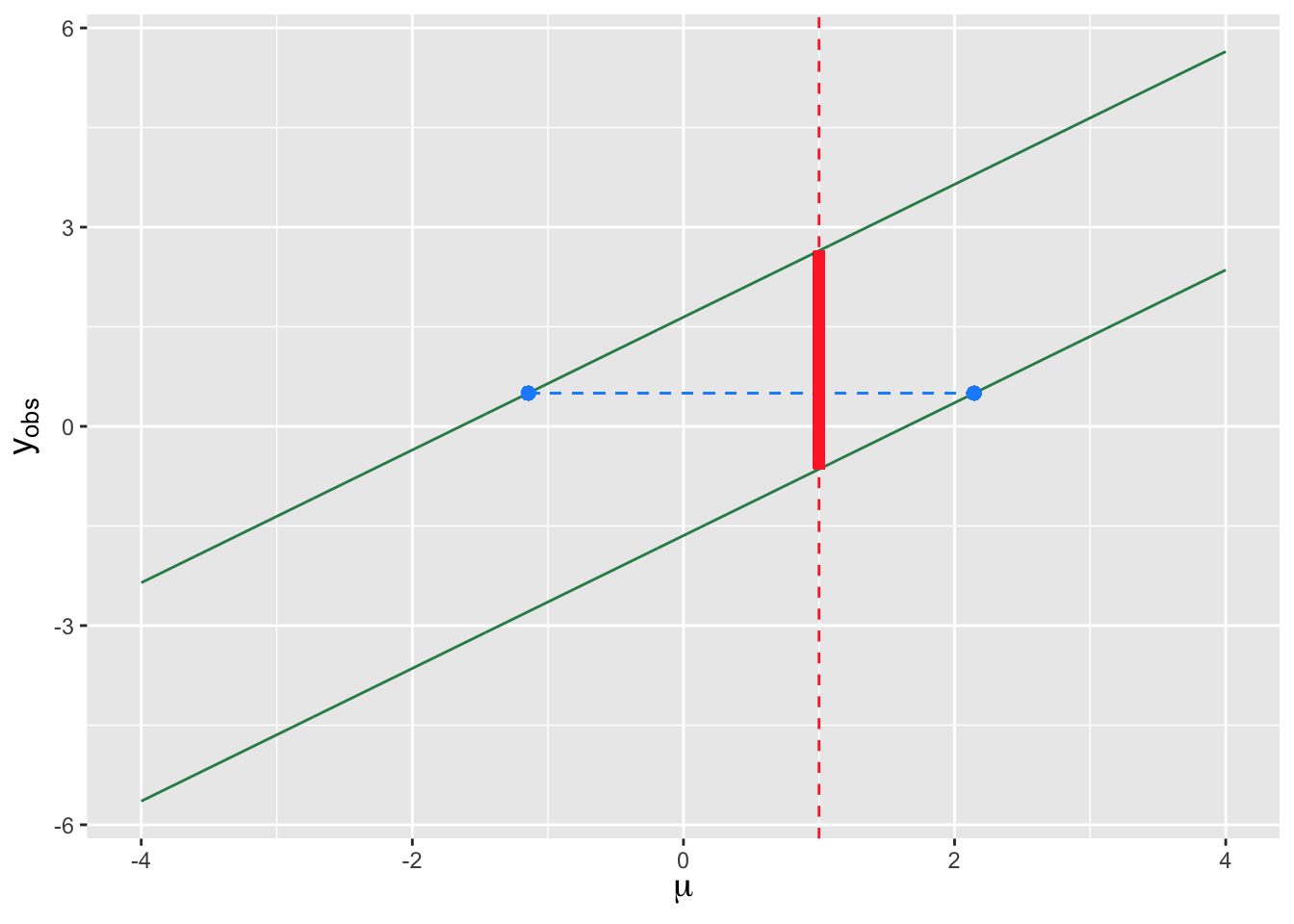
Figure 3.7: An illustration of the relationship between hypothesis testing and confidence interval estimation for a continuous sampling distribution (here, a normal distribution with known variance). The two parallel green lines define rejection-region boundaries for a two-sided test with null hypothesis parameter value \(\mu\). Assume \(\mu = 1\): the dashed red lines indicate the values of \(y_{\rm obs}\) in the rejection region, while the solid red line indicates the values of \(y_{\rm obs}\) in the acceptance region (where we fail to reject the null). The horizontal dashed blue line shows the confidence interval constructed for a given value of \(y_{\rm obs}\). Given \(\mu\), the probability of sampling a statistic in the acceptance region is exactly \(1-\alpha\), and thus the coverage of confidence intervals will also be exactly \(1-\alpha\).
When we work with discrete sampling distributions, the overall picture is similar, but we sometimes need to make what we will dub “discreteness corrections” so that the codes we use generate the correct results. Figure 3.8 is an analogue to Figure 3.7 in which we illustrate the relationship between confidence intervals and hypothesis tests for a situation in which we conduct \(k = 10\) binomial trials. Because the statistic is discretely valued, the acceptance-region boundaries are step functions, but this is not the only change introduced with discrete distributions:
In the continuous case, the probability of sampling a datum that lies within the acceptance region for a given value of \(\theta\) is exactly \(1 - \alpha\). In the discrete case, that probability is \(\geq 1 - \alpha\). (And it will rarely, if ever, be the case that the probability masses within the acceptance region will sum to exactly \(1 - \alpha\)…although that sum will trend towards \(1 - \alpha\) as the sample size and/or the number of trials increases. This motivates our use of the word “level,” as in “we conduct a level-\(\alpha\) test,” rather than “size.” For a size-\(\alpha\) test, the probability of sampling a statistic value in the acceptance region is, by definition, exactly \(1-\alpha\), while for a level-\(\alpha\) test, it is \(\geq 1 - \alpha\).)
Because the probability of sampling a datum in the acceptance region is equal to the confidence interval coverage, the coverage will also be \(\geq 1 - \alpha\).
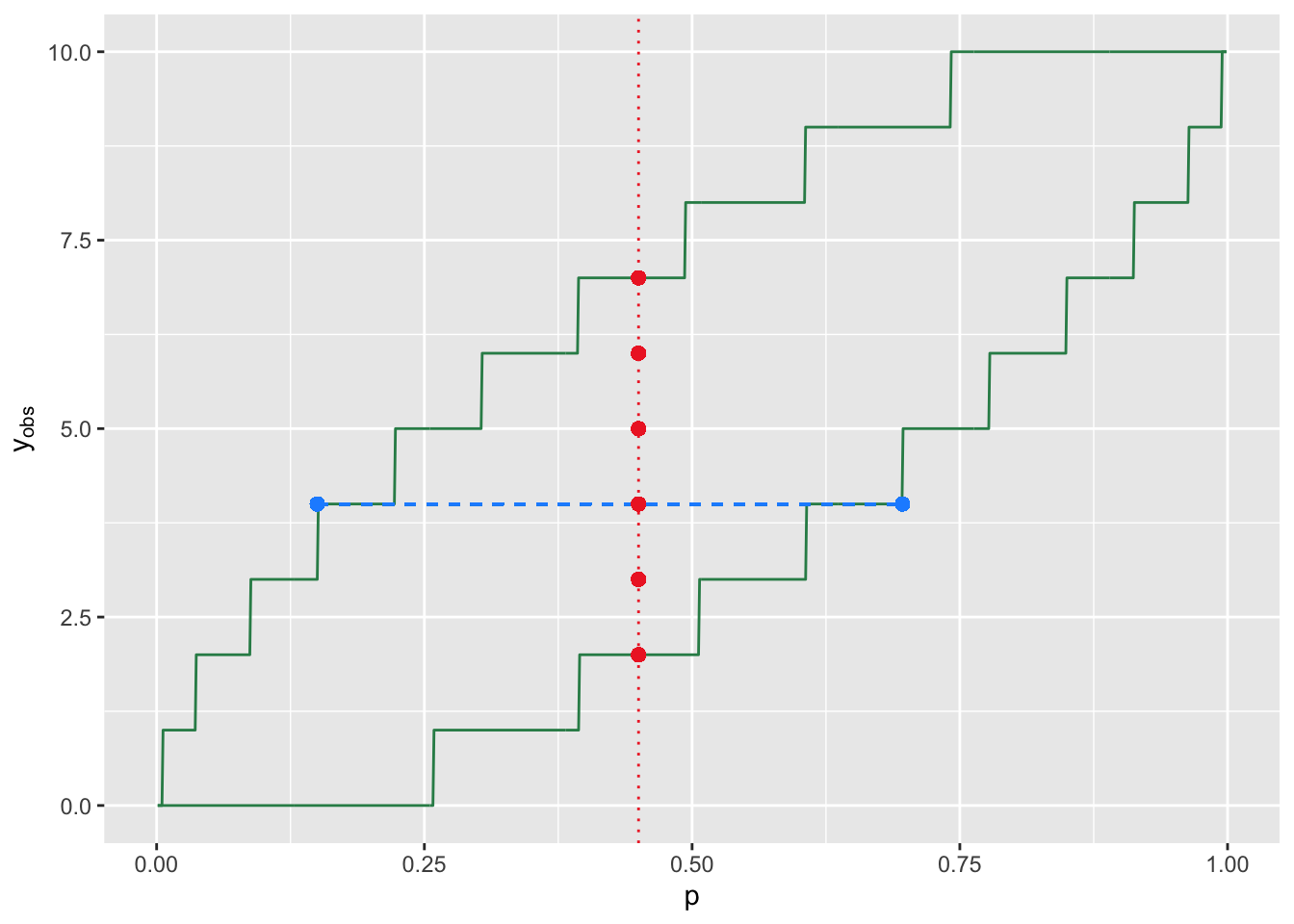
Figure 3.8: An illustration of the relationship between hypothesis testing and confidence interval estimation for a discrete sampling distribution (here, a binomial distribution with \(k=10\)). The two green lines define rejection-region boundaries for a two-sided test with null hypothesis parameter value \(p\). Assume \(p = 0.45\): the red dots indicates the values of \(y_{\rm obs}\) in the acceptance region (where we fail to reject the null). The horizontal dashed blue line shows the confidence interval constructed for a given value of \(y_{\rm obs}\). Given \(p\), the probability of sampling a statistic in the acceptance region is generally greater than \(1-\alpha\), and thus the coverage of confidence intervals, which has the same value, will also be generally greater than \(1-\alpha\).
The blue dashed line in Figure 3.8 is an example of
a confidence interval (specifically for \(y_{\rm obs} = 4\)). In order to
construct an interval like this, we would use a uniroot()-style code
as we have before, but with the following changes.
- If we are determining a lower bound \(\hat{\theta}_L\) in a situation where \(E[Y]\) increases with \(\theta\), we need to replace \(y_{\rm obs}\) in the input to
uniroot()with the next smaller value in the distribution’s domain (e.g., \(y_{\rm obs} - 1\) for a binomially distributed statistic). - If we are determining an upper bound \(\hat{\theta}_U\) in a situation where \(E[Y]\) decreases with \(\theta\), we need to replace \(y_{\rm obs}\) in the input to
uniroot()with the next smaller value in the distribution’s domain (e.g., \(y_{\rm obs} - 1\) for a negative binomially distributed statistic).
We note that for the specific case of the binomial distribution, the confidence intervals that we construct are dubbed exact, or Clopper-Pearson, intervals. Because binomial distributions have historically been difficult to work with analytically, a number of algorithms have been developed through the years for constructing approximate confidence intervals for binomial probabilities. (See, e.g., this Wikipedia page for examples.) It is our opinion that there is no reason to utilize any of these algorithms when one can compute exact intervals, particularly since the coverages of exact intervals are easily derived for any given value \(p\). However, for completeness, we illustrate how one would construct the most-commonly used approximating interval, the Wald interval, in an example below.
3.7.1 Confidence Interval for the Binomial Success Probability
Assume that we sample \(n\) iid data from a binomial distribution with number of trials \(k\) and probability \(p\). Then, as shown above, \(Y = \sum_{i=1}^n X_i \sim\) Binom(\(nk,p\)); our observed test statistic is \(y_{\rm obs} = \sum_{i=1}^n x_i\). For this statistic, \(E[Y] = nkp\) increases with \(p\), so \(q = 1-\alpha/2\) maps to the lower bound, while \(q = \alpha/2\) maps to the upper bound.
set.seed(101)
alpha <- 0.05
n <- 12
k <- 5
p <- 0.4
X <- rbinom(n,size=k,prob=p)
f <- function(p,y.obs,n,k,q)
{
pbinom(y.obs,size=n*k,prob=p)-q
}
uniroot(f,interval=c(0,1),y.obs=sum(X)-1,n,k,1-alpha/2)$root # note correction## [1] 0.2459379## [1] 0.5010387We find that the interval is \([\hat{p}_L,\hat{p}_U] = [0.246,0.501]\), which overlaps the true value of 0.4. (See Figure 3.9.) Note that, unlike in Chapter 2, the interval over which we search for the root is [0,1], which is the range of possible values for \(p\).
We can compute the coverage of this interval following the prescription given above:
y.rr.lo <- qbinom(alpha/2,n*k,p)
y.rr.hi <- qbinom(1-alpha/2,n*k,p)
sum(dbinom(y.rr.lo:y.rr.hi,n*k,p))## [1] 0.9646363Due to the discreteness of the binomial distribution, the true coverage of our two-sided intervals, in this particular circumstance, is 96.5%, not 95%.
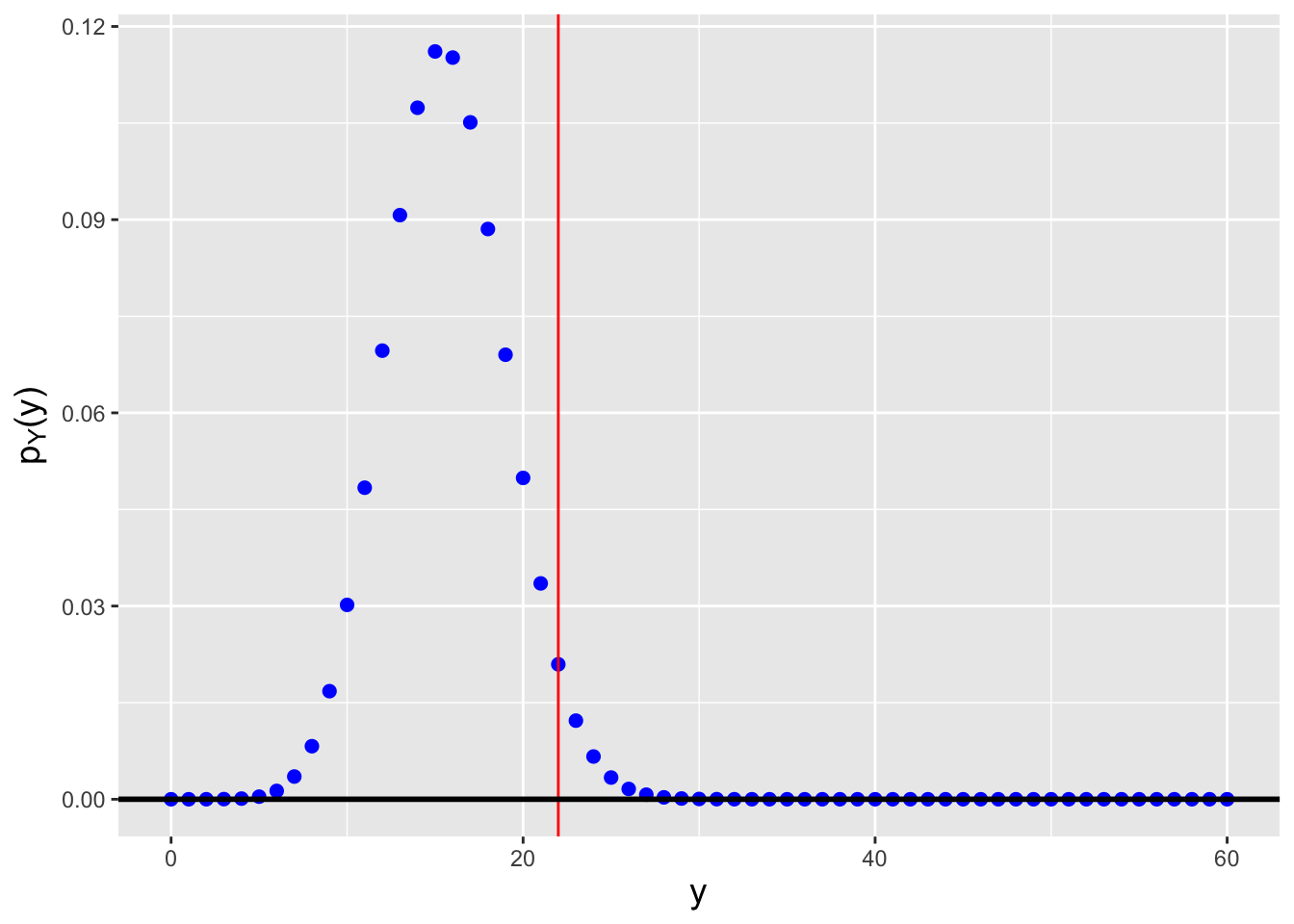
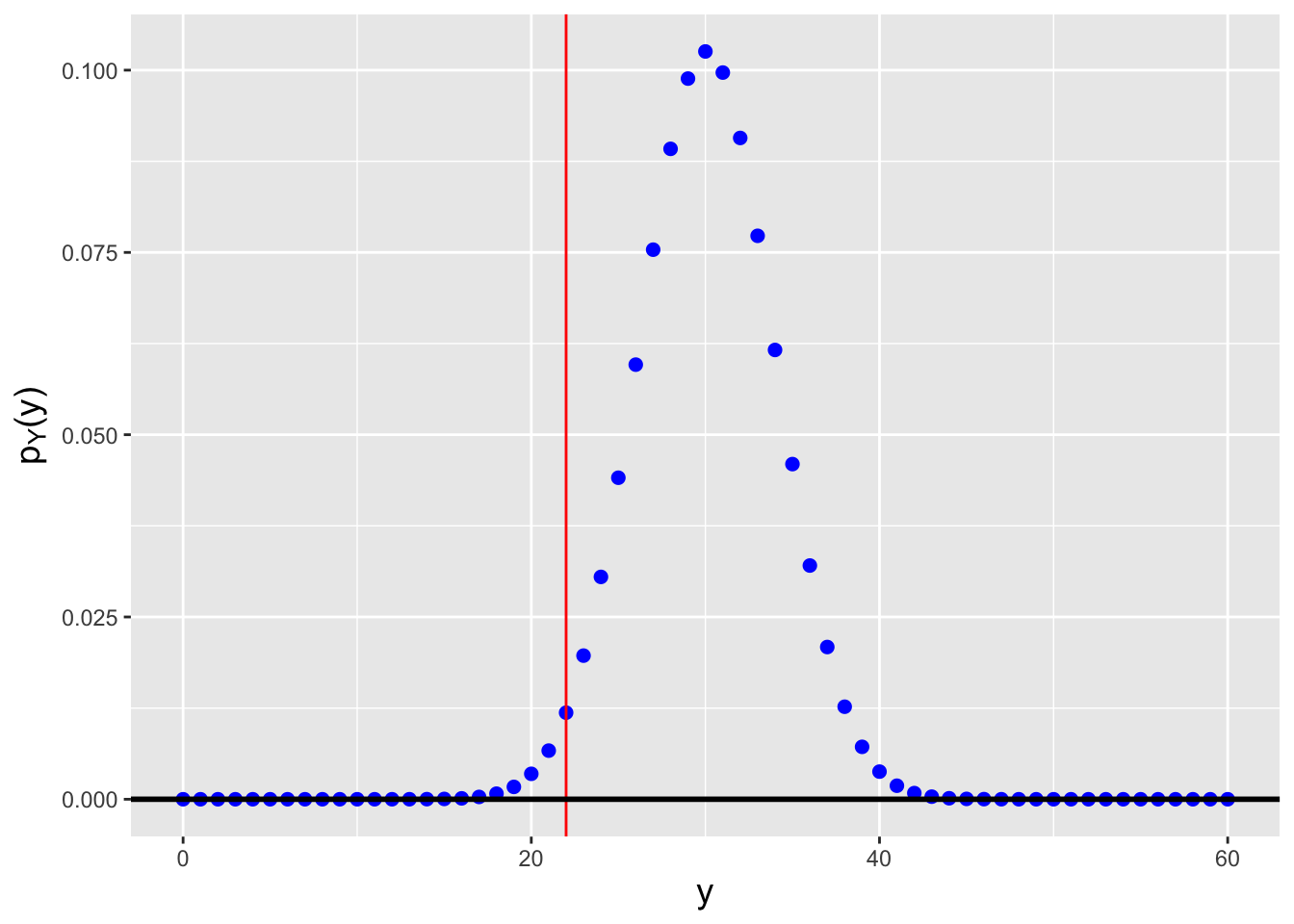
Figure 3.9: Probability mass functions for binomial distributions for which \(n \cdot k= 12 \cdot 5 = 60\) and (left) \(p=0.246\) and (right) \(p=0.501\). We observe \(y_{\rm obs} = \sum_{i=1}^n x_i = 22\) successes and we want to construct a 95% confidence interval. \(p=0.246\) is the smallest value of \(p\) such that \(F_Y^{-1}(0.975) = 22\), while \(p=0.501\) is the largest value of \(p\) such that \(F_Y^{-1}(0.025) = 22\).
3.7.2 Confidence Interval for the Negative Binomial Success Probability
Let’s assume that we have performed \(n = 10\) separate negative binomial trials, each with a target number of successes \(s\), and recorded the number of failures \(X_1,\ldots,X_{n}\) for each. Further, assume that the probability of success is \(p\). Below we will show how to compute the confidence interval for \(p\), but before we start, we recall that \(Y = \sum_{i=1}^n X_i\) is a negative binomially distributed random variable for \(ns\) successes and probability of success \(p\). Here, \(E[Y] = s(1-p)/p\)…as \(p\) increases, \(E[Y]\) decreases. Thus when we adapt the confidence interval code we use for binomially distributed data, we need to switch the mapping of \(q = 1-\alpha/2\) and \(q = \alpha/2\) to the upper and lower bounds, respectively.
set.seed(101)
alpha <- 0.05
n <- 12
s <- 5
p <- 0.4
X <- rnbinom(n,size=s,prob=p)
f <- function(p,y.obs,n,s,q)
{
pnbinom(y.obs,size=n*s,prob=p)-q
}
uniroot(f,interval=c(0.0001,1),y.obs=sum(X),n,s,alpha/2)$root## [1] 0.3255305## [1] 0.4853274The confidence interval is \([\hat{p}_L,\hat{p}_U] = [0.326,0.485]\), which overlaps the true value 0.4. We note that in the code, we change the lower bound on the interval from 0 (in the binomial case) to 0.0001 (something suitably small but non-zero): a probability of success of 0 maps to an infinite number of failures, which
Rcannot tolerate!
We can compute the coverage of this interval following the prescription given above:
y.rr.lo <- qnbinom(1-alpha/2,n*s,p)
y.rr.hi <- qnbinom(alpha/2,n*s,p)
sum(dnbinom(y.rr.lo:y.rr.hi,n*s,p))## [1] 0.9510741Due to the discreteness of the binomial distribution, the true coverage of our two-sided intervals is 95.1%, not 95%.
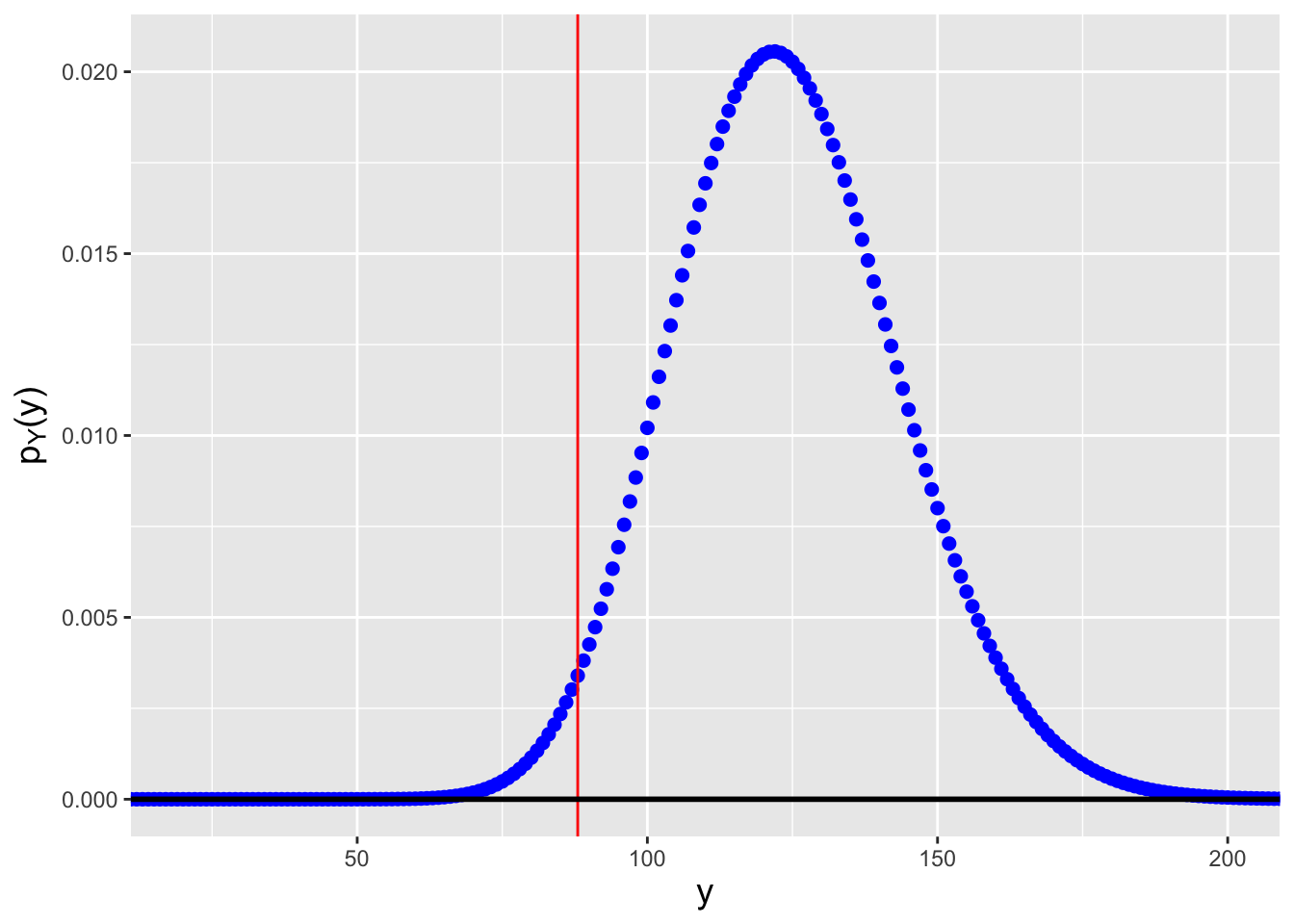
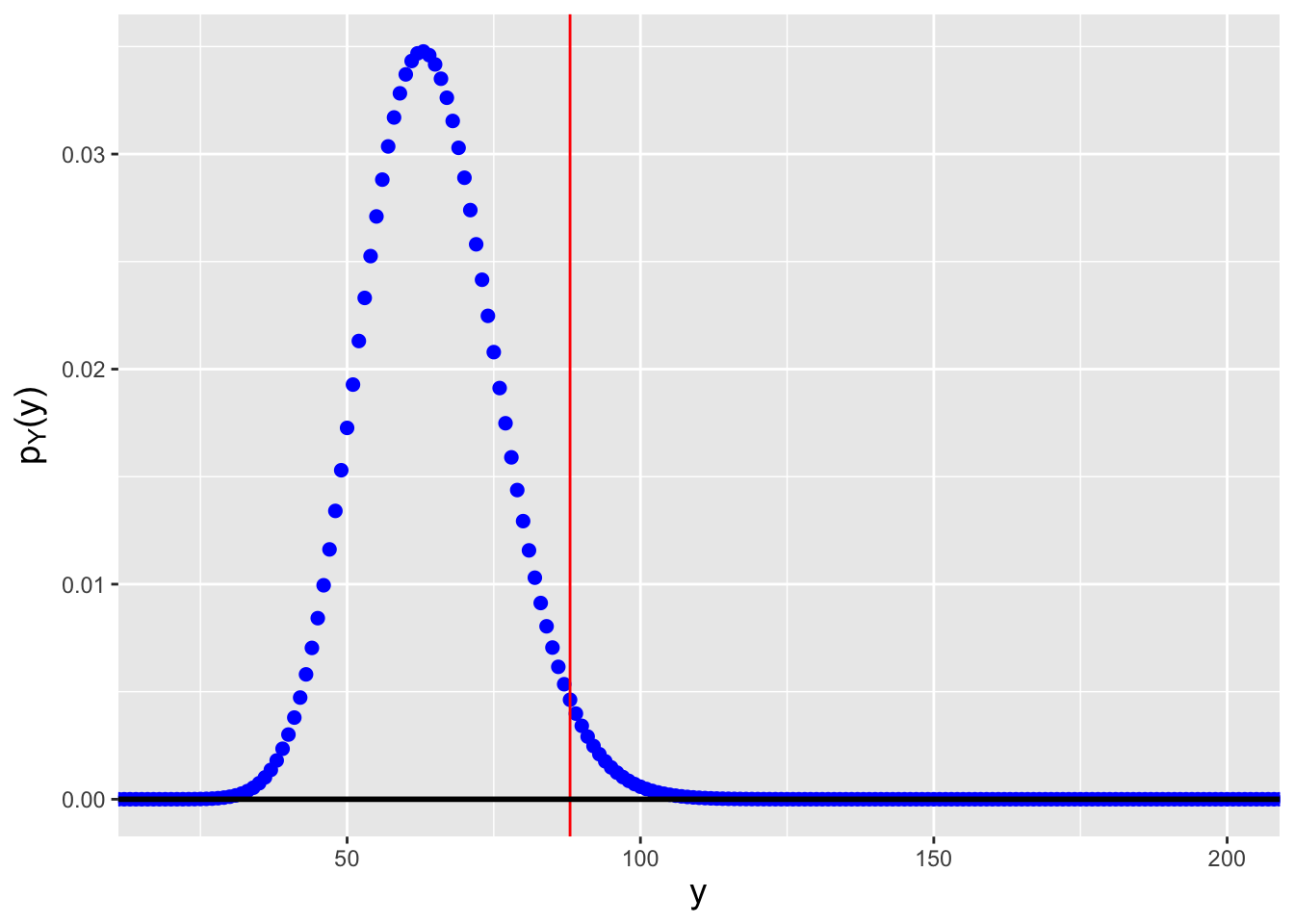
Figure 3.10: Probability mass functions for negative binomial distributions for which \(n \cdot s = 12 \cdot 5 = 60\) and (left) \(p=0.326\) and (right) \(p=0.485\). We observe \(y_{\rm obs} = \sum_{i=1}^n x_i = 88\) failures and we want to construct a 95% confidence interval. \(p=0.326\) is the smallest value of \(p\) such that \(F_Y^{-1}(0.025) = 88\), while \(p=0.485\) is the largest value of \(p\) such that \(F_Y^{-1}(0.975) = 88\).
3.7.3 Wald Interval for the Binomial Success Probability
Let’s assume that we have sampled \(n\) iid binomial variables with number of trials \(k\) and probability of success \(p\). When \(k\) is sufficiently large and \(p\) is sufficiently far from 0 or 1, we can assume that \(\bar{X}\) has a distribution whose shape is approximately that of a normal distribution, with mean \(E[\bar{X}] = kp\) and with variance and standard error \[ V[\bar{X}] = \frac{kp(1-p)}{n} ~~~ \mbox{and} ~~~ se(\bar{X}) = \sqrt{V[\bar{X}]} = \sqrt{\frac{kp(1-p)}{n}} \,. \] Furthermore, we can assume that \(\hat{p} = \bar{X}/k\) is approximately normally distributed, with mean \(p\), variance \(V[\hat{p}] = V[\bar{X}]/k^2 = p(1-p)/nk\), and standard error \(\sqrt{p(1-p)/nk}\). Given this information, it is simple to express, e.g., an approximate two-sided \(100(1-\alpha)\)% confidence interval for \(p\): \[ \hat{p} \pm z_{1-\alpha/2} se(\hat{p}) ~~ \Rightarrow ~~ \left[ \hat{p} - z_{1-\alpha/2} \sqrt{\frac{p(1-p)}{nk}} \, , \, \hat{p} + z_{1-\alpha/2} \sqrt{\frac{p(1-p)}{nk}} \right] \,, \] where \(z_{1-\alpha/2} = \Phi^{-1}(1-\alpha/2)\). However, we don’t actually know the true value of \(p\)…so we plug in \(p = \hat{p}\).
This is the so-called Wald interval that is typically provided to students in introductory statistics courses, although it is typically provided assuming \(n = 1\) and assuming that \(\alpha = 0.05\): \[ \left[ \hat{p} - 1.96 \sqrt{\frac{\hat{p}(1-\hat{p})}{k}} \, , \, \hat{p} + 1.96 \sqrt{\frac{\hat{p}(1-\hat{p})}{k}} \right] \,, \] where in this case \(\hat{p} = X/k\).
What is the Wald interval for the situation provided in the first example above?
set.seed(101)
alpha <- 0.05
n <- 12
k <- 5
p <- 0.4
X <- rbinom(n,size=k,prob=p)
z <- qnorm(1-alpha/2)
p.hat <- sum(X)/(n*k)
p.hat - z*sqrt(p.hat*(1-p.hat)/(n*k))## [1] 0.2447328## [1] 0.4886005We can compare these values to those generated in the first example: \([0.236,0.501]\). Here, the interval is smaller relative to the Clopper-Pearson interval, and thus the coverage for \(p = 0.4\) (which we would have to estimate via simulation) will be smaller as well.
3.8 Hypothesis Testing
Recall: a hypothesis test is a framework to make an inference about the value of a population parameter \(\theta\). The null hypothesis \(H_o\) is that \(\theta = \theta_o\), while possible alternatives \(H_a\) are \(\theta \neq \theta_o\) (two-tail test), \(\theta > \theta_o\) (upper-tail test), and \(\theta < \theta_o\) (lower-tail test). For, e.g., a one-tail test, we reject the null hypothesis if the observed test statistic \(y_{\rm obs}\) falls outside the bound given by \(y_{RR}\), which is a solution to the equation \[ F_Y(y_{RR} \vert \theta_o) - q = 0 \,, \] where \(F_Y(\cdot)\) is the cumulative distribution function for the statistic \(Y\) and \(q\) is an appropriate quantile value that is determined using the hypothesis test reference table introduced in section 17 of Chapter 1. Note that the hypothesis test framework only allows us to make a decision about a null hypothesis; nothing is proven.
In the previous chapter, we utilized \(\bar{X}\) when testing hypotheses about the normal mean \(\mu\). This is a principled choice for a test statistic\(-\)after all, \(\bar{X}\) is the MLE for \(\mu-\)but we do not yet know whether or not we can choose a better one. Can we differentiate hypotheses more easily if we use a test statistic other than \(\bar{X}\)?
To help answer this question, we now introduce a method for defining the most powerful test of a simple null hypothesis versus a simple alternative hypothesis: \[ H_o : \theta = \theta_o ~~\mbox{and}~~ H_a : \theta = \theta_a \,. \] Note that the word “simple” has a precise meaning here: it means that when we set \(\theta\) to a particular value, we are completely fixing the shape and location of the pmf or pdf from which data are sampled. If, for instance, we are dealing with a normal distribution with unknown variance \(\sigma^2\), the hypothesis \(\mu = \mu_o\) would not be simple, since the width of the pdf can still vary: the shape is not completely fixed. (The hypothesis \(\mu = \mu_o\) with variance unknown is dubbed a composite hypothesis. We will examine how to work with composite hypotheses in the next chapter.) For a given test level \(\alpha\), the Neyman-Pearson lemma states that the test that maximizes the power has a rejection region of the form \[ \lambda_{NP} = \frac{\mathcal{L}(\theta_o \vert \mathbf{x})}{\mathcal{L}(\theta_a \vert \mathbf{x})} < c(\alpha) \,, \] where \(c\) is a constant whose value depends on \(\alpha\) that we have to determine. While this formulation initially appears straightforward, it is in fact not necessarily clear how to derive \(c(\alpha)\). However: when we work with distributions that belong to the exponential family, we don’t need to! The NP lemma utilizes the likelihood function, so in this situation it is implicitly telling us that the best statistic for differentiating between two simple hypotheses is a sufficient statistic. We simply determine a sufficient statistic and and use its sampling distribution to define a hypothesis test via the procedure we have laid out in previous chapters. Full stop. (What if the distribution we are working with is not a member of the exponential family? We would need to determine the sampling distribution of \(\lambda_{NP}\) itself, something most easily done via the use of simulations. We illustrate this in an example below.)
For instance, when we draw \(n\) iid data from a binomial distribution, the sufficient statistic \(\sum_{i=1}^n X_i\) has a known and easily utilized sampling distribution\(-\)namely, Binom(\(nk,p\))\(-\)while \(\bar{X} = (\sum_{i=1}^n X_i)/n\) does not. So we would utilize \(Y = \sum_{i=1}^n X_i\). (Note that it ultimately doesn’t matter which function of a sufficient statistic we use: if we can carry out the math, we will end up with tests that have the same power and result in the same \(p\)-values. It would be very problematic if this wasn’t the case: we’d have to “fish around” to determine which function of a sufficient statistic would give us the best test, which clearly would not be a good situation to find ourselves in.)
Let’s assume that we use \(Y = \sum_{i=1}^n X_i\) to define, e.g., a lower-tail test \(H_o : p = p_o\) versus \(H_a : p = p_a < p_o\). Since \(E[Y] = nkp\) increases with \(p\), we can go to the hypothesis test reference tables and write (in code) that
We see that our rejection region boundary depends on the value of \(p_o\), but not on the value of \(p_a\). This means that the test we define above is the most-powerful test regardless of the value \(p_a < p_o\). We have thus constructed a uniformly most powerful (or UMP) test for disambiguating the simple hypotheses \(H_o : p = p_o\) and \(H_a : p = p_a < p_o\). It is typically the case that when we use the NP lemma to define a most powerful test for \(\theta_o\) versus \(\theta_a\), we end up defining a UMP test as well. (That is because the families of distributions that we work with typically exhibit so-called monotone likelihood ratios [or MLRs]. For more information on MLRs and UMPs, the interested reader should look at the Karlin-Rubin theorem.)
We note that we cannot use the NP lemma to construct most powerful two-tail hypothesis tests. When we construct a two-tail test, it is convention to define one rejection region boundary assuming \(q = \alpha/2\) and the other assuming \(q = 1 - \alpha/2\). But that is just convention; we could put \(\alpha/10\) on “one side” and \(1-9\alpha/10\) on the other, etc., and in general we cannot guarantee that any one way of splitting \(\alpha\) will yield a more powerful test in a given situation than any other possible split.
We conclude our present discussion of hypothesis tests with an overview of how working with a discrete sampling distribution affects the computation of \(p\)-values and test power.
In the last section, we introduced the idea of a “discreteness correction”; for confidence interval calculations, this involved changing the observed statistic value to the next lower value in the domain of the sampling distribution when estimating a lower interval bound (with \(E[Y]\) increasing with \(\theta\)) or when estimating an upper interval bound (with \(E[Y]\) decreasing with \(\theta\)). (For the binomial and negative binomial distributions, this means changing \(y_{\rm obs}\) to \(y_{\rm obs}-1\).) What are the discreteness corrections that we need to make when performing hypothesis tests? First, there are none when computing rejection-region boundaries. Second, when computing \(p\)-values, we change the observed statistic value to the next lower value in the domain of the sampling distribution when performing
- upper-tail tests where \(E[Y]\) increases with \(\theta\) and
- lower-tail tests where \(E[Y]\) decreases with \(\theta\).
Last, when computing test power, we change the derived rejection-region boundary to the next lower value in the domain of the sampling distribution when performing
- upper-tail tests where \(E[Y]\) decreases with \(\theta\) and
- lower-tail tests where \(E[Y]\) increases with \(\theta\).
3.8.1 UMP Test: Exponential Distribution
Let’s suppose we sample \(n = 3\) iid data from the exponential distribution \[ f_X(x) = \frac{1}{\theta} e^{-x/\theta} \,, \] for \(x \geq 0\) and \(\theta > 0\), and we wish to define the most powerful test of the simple hypotheses \(H_o : \theta_o = 2\) and \(H_a : \theta_a = 1\). We observe the values \(\mathbf{x}_{\rm obs} = \{0.215,1.131,2.064\}\), and we assume \(\alpha = 0.05\).
We begin by determining a sufficient statistic: \[ \mathcal{L}(\theta \vert \mathbf{x}) = \prod_{i=1}^3 \frac{1}{\theta} e^{-x_i/\theta} = \frac{1}{\theta^3} e^{(\sum_{i=1}^3 x_i)/\theta} \,. \] We identify \(Y = \sum_{i=1}^3 X_i\) as a sufficient statistic. The next question is whether we can determine the sampling distribution for \(Y\). The moment-generating function for each of the \(X_i\)’s is \[ m_{X_i}(t) = (1 - \theta t)^{-1} \,, \] and so the mgf for \(Y\) is \[ m_Y(t) = \prod_{i=1}^3 m_{X_i}(t) = (1 - \theta t)^{-3} \,, \] We (might!) recognize this as the mgf for a Gamma(3,\(\theta\)) distribution. (The gamma distribution will be officially introduced in Chapter 4.) So: we know the sampling distribution for \(Y\), and we can use it to define the most powerful test. To reiterate: the only thing that the NP lemma is doing for us here is guiding our selection of a test statistic. Beyond that, we construct the test using the framework we already learned in Chapters 1 and 2.
Because \(\theta_a < \theta_o\), we define a lower-tail test. And since \(E[Y] = 3\theta\) increases with \(\theta\), we utilize the formulae from the hypothesis test reference tables that are on the “yes” line. The rejection-region boundary is thus \[ y_{\rm RR} = F_Y^{-1}(\alpha \vert \theta_o) \,, \] which in code is
## [1] 3.41## [1] 1.635383Our observed statistic is \(y_{\rm obs} = 3.410\) and the rejection-region boundary is 1.635: we fail to reject the null and conclude that \(\theta_o = 2\) is a plausible value of \(\theta\).
We note that because \(y_{\rm RR}\) is not a function of \(\theta_a\), we have not only defined the most powerful test, but we have also defined a uniformly most powerful test for all alternative hypotheses \(\theta_a < \theta_o\).
What is the \(p\)-value, and what is the power of the test if \(\theta = 1.5\)?
According to the hypothesis test reference tables, the \(p\)-value is \[ p = F_Y(y_{\rm obs} \vert \theta_o) \,, \] which in code is
## [1] 0.2440973The \(p\)-value is 0.244, which is greater than \(\alpha\), as we expect.
The test power is \[ {\rm power}(\theta) = F_Y(y_{\rm RR} \vert \theta) \,, \] which in code is
## [1] 0.09762911The power is 0.097…only 9.7% of the time will we reject the null hypothesis \(\theta_o = 2\) when \(\theta\) is actually 1.5.
3.8.2 UMP Test: Negative Binomial Distribution
Let’s assume that we sample \(n = 5\) data from a negative binomial distribution \[ p_X(x) = \binom{x+s-1}{x} p^s (1-p)^x \,, \] with \(x \in \{0,1,\ldots,\infty\}\) being the observed number of failures prior to observed the \(s^{\rm th}\) success, \(p \in (0,1]\), and \(s = 3\) successes. We wish to define the most powerful test of the simple hypotheses \(H_o : p_o = 0.5\) and \(H_a : p_a = 0.25\). We observe the values \(\mathbf{x}_{\rm obs} = \{5,3,10,12,4\}\), and we assume \(\alpha = 0.05\).
As in the last example, we begin by determining a sufficient statistic: \[ \mathcal{L}(\theta \vert \mathbf{x}) = \prod_{i=1}^5 \binom{x_i+s-1}{x_i} p^s (1-p)^x_i \propto \prod_{i=1}^5 p^s (1-p)^x_i = p^{ns} (1-p)^{\sum_{i=1}^5 x_i} \,. \] We identify \(Y = \sum_{i=1}^5 X_i\) as a sufficient statistic. Earlier in the chapter, we determined that if the \(X_i\)’s are iid draws from a negative binomial distribution with parameters \(p\) and \(s\), then the sum is also negative binomially distributed, with parameters \(p\) and \(ns\). So: we know the sampling distribution for \(Y\), and we can use it to define the most powerful test.
Because \(p_a < p_o\), we will define a lower-tail test. And since \(E[Y] = s(1-p)/p\) decreases with \(p\), we will utilize the formulae from the hypothesis test reference tables that are on the “no” line (and we will reject the null hypothesis if \(y_{\rm obs} > y_{\rm RR}\)).
The rejection-region boundary is \[ y_{\rm RR} = F_Y^{-1}(1-\alpha \vert p_o) \,, \] which in code is
## [1] 34## [1] 25Our observed statistic is \(y_{\rm obs} = 34\) and the rejection-region boundary is 25: we reject the null hypothesis and state that there is sufficient evidence to conclude that \(p < 0.5\).
We note that because \(y_{\rm RR}\) is not a function of \(p_a\), we have not only defined the most powerful test, but we have also defined a uniformly most powerful test for all alternative hypotheses \(p_a < p_o\).
What is the \(p\)-value, and what is the power of the test if \(p = 0.3\)?
According to the hypothesis test reference tables (and the description of discreteness corrections given above), the \(p\)-value is \[ p = 1 - F_Y(y_{\rm obs}-1 \vert p_o) \,, \] which in code is
## [1] 0.002757601The \(p\)-value is 0.0028, which is less than \(\alpha\): we would decide to reject the null hypothesis.
The test power (a calculation that in this instance does not require a discreteness correction) is \[ {\rm power}(\theta) = 1 - F_Y(y_{\rm RR} \vert p) \,, \] which in code is
## [1] 0.8074482We find that the power is 0.807…80.7% of the time will we reject the null hypothesis \(p = 0.5\) when \(p\) is actually 0.3 (and when \(n = 5\) and \(s = 3\)).
3.8.3 Defining a UMP Test for the Normal Population Mean
In Chapter 2, we use the statistic \(\bar{X}\) as the basis for testing hypotheses about the normal population mean, \(\mu\). We justified this choice because, at the very least, \(\hat{\mu}_{MLE} = \bar{X}\), so it is a principled choice. However, beyond that, we did not (and indeed could not) provide any further justification. Is \(\bar{X}\) the basis of the UMP for \(\mu\)?
Recall that the NP lemma does not apply if there are two freely varying parameters. The NP lemma applies to simple hypotheses, where the hypotheses uniquely specify the population from which data are drawn. Here, even if we set \(H_o: \mu = \mu_o\) and \(H_a: \mu = \mu_a\), \(\sigma^2\) can still freely vary. (So, technically, these hypotheses are composite hypotheses.) So to go further here, we must assume \(\sigma^2\) is known.
When \(\sigma^2\) is known, we can factorize the likelihood as \[ \mathcal{L}(\mu,\sigma^2 \vert \mathbf{x}) = \underbrace{\exp\left(\frac{\mu}{\sigma^2}\sum_{i=1}^n x_i\right)\exp\left(-\frac{n\mu^2}{2\sigma^2}\right)}_{g(\sum x_i,\mu)} \cdot \underbrace{(2 \pi \sigma^2)^{-n/2} \exp\left(-\frac{1}{2\sigma^2}\sum_{i=1}^n x_i^2\right)}_{h(\mathbf{x})} \,, \] and identify \(Y = \sum_{i=1}^n X_i\) as a sufficient statistic. We know from using the method of moment-generating functions that the sum of \(n\) iid normal random variables is itself a normal random variable with mean \(n\mu\) and variance \(n\sigma^2\), so \(Y \sim \mathcal{N}(n\mu,n\sigma^2)\).
Let’s assume that \(\mu_a > \mu_o\), or, in other words, that we are performing an upper-tail test. Given that \(E[Y] = n\mu\), we know that we are on the “yes” line of the hypothesis test reference tables, so the rejection region is \[ Y > y_{\rm RR} = F_Y^{-1}(1-\alpha,n\mu_o,n\sigma^2) \,, \] or, in code,
qnorm(1-alpha,n*mu.o,n*sigma2)The rejection-region boundary does not depend on \(\mu_a\), so we have defined a uniformly most powerful test of \(\mu = \mu_o\) versus \(\mu = \mu_a > \mu_o\).
“But wait. What about \(\bar{X}\)?”
Recall that a function of a sufficient statistic is itself a sufficient statistic, so we could also use \(Y' = \bar{X} = Y/n\) as our statistic, particularly as we do know its sampling distribution: \(\mathcal{N}(\mu,\sigma^2/n)\). Thus \[ Y' > y_{\rm RR}' = F_Y^{-1}(1-\alpha,\mu_o,\sigma^2/n) \,, \] or, in code,
qnorm(1-alpha,mu.o,sigma2/n)“But…\(y_{\rm RR}\) and \(y_{\rm RR}'\) do not have the same value!”
This is fine: \(Y\) and \(Y'\) don’t have the same value either. The key point is that when we compute, e.g., \(p\)-values given observed data, they will be the same in both cases. And the test power will be the same. We can use any function of a sufficient statistic to define our test; in practice, we will use any function of a sufficient statistic for which we know the sampling distribution. Here we know the distributions for both the sample sum and the sample mean; in other situations (like when we are working with binomially distributed data), we will not.
Now, what if \(\sigma^2\) is unknown? We discuss this possibility in the next chapter, when we introduce the likelihood ratio test.
3.8.4 Defining a Test That is Not Uniformly Most Powerful
Let’s assume we draw one datum \(X\) from a normal distribution with mean \(\mu\) and variance \(\mu^2\), and we wish to test \(H_o : \mu = \mu_o = 1\) versus \(H_a : \mu = \mu_a\). Can we define a uniformly most powerful test of these hypotheses?
To try to do this, we utilize the NP lemma. However, there is an immediate issue that arises: here, there are two sufficient statistics that are identified via factorization (\(\sum_{i=1}^n X_i\) and \(\sum_{i=1}^n X_i^2\)), but just one parameter (\(\mu\)). So we cannot circumvent working directly with the likelihood ratio: \[\begin{align*} \frac{\mathcal{L}(\theta_o \vert \mathbf{x})}{\mathcal{L}(\theta_a \vert \mathbf{x})} = \frac{f_X(x \vert \theta_o)}{f_X(x \vert \theta_a)} = \mu_a \exp\left(-\frac{(x-1)^2}{2}+\frac{(x-\mu_a)^2}{2\mu_a^2}\right) \,. \end{align*}\] To reject the null hypothesis, the ratio must be less than some constant \(c(\alpha)\). First, we can divide both sides of the inequality by \(\mu_a\) (which is a set constant), so that now we reject the null if \[\begin{align*} \exp\left(-\frac{(x-1)^2}{2}+\frac{(x-\mu_a)^2}{2\mu_a^2}\right) < c'(\alpha) \,. \end{align*}\] We then take the natural logarithm of each side; we would reject the null if \[\begin{align*} -\frac{(x-1)^2}{2}+\frac{(x-\mu_a)^2}{2\mu_a^2} < c''(\alpha) \,. \end{align*}\] It turns out that for the test to be uniformly most powerful, we would have to perform further manipulations so as to isolate \(x\) on the left-hand side of the inequality, with only constants appearing on the right-hand side (i.e., we would need to simplify this expression such that it achieves the form \(x < k\) or \(x > k\)). Here, that is impossible to do, meaning that the value of the rejection region boundary changes as \(\mu_a\) changes. Thus while we can define the most powerful test of \(H_o : \mu = \mu_o = 1\) versus \(H_a : \mu = \mu_a\), that test is not a uniformly most powerful one.
3.8.5 Estimating a \(p\)-Value via Simulation
Let’s assume that we sample \(n\) iid data from a distribution whose probability density function is \[\begin{align*} f_X(x \vert \theta) = \theta x^{\theta-1} \,, \end{align*}\] where \(x \in [0,1]\) and \(\theta > 0\). Furthermore, let’s assume we wish to test \(H_o : \theta = \theta_o = 1\) versus \(H_a : \theta = \theta_a = 2\).
The Neyman-Pearson lemma tells us that a sufficient statistic will provide the basis for the most powerful test. Likelihood factorization indicates that one such statistic is \[\begin{align*} Y = \prod_{i=1}^n X_i \,, \end{align*}\] but, since functions of sufficient statistics are themselves sufficient, we could also utilize \[\begin{align*} Y = \log \prod_{i=1}^n X_i = \sum_{i=1}^n \log X_i \,. \end{align*}\] We will choose to utilize \(Y'\) because in general, summations are computationally easier to work with than products. However…we do not know the sampling distribution for \(Y\). So we simulate. In a simulation, we do the following:
- we sample data from the original distribution given the null;
- we form the statistic and store its value;
- we repeat steps 1 and 2 a large number of times; and
- we see how often the simulated statistic value is (in this case) greater than the observed value…that proportion is our estimated \(p\)-value.
Below we carry out a simulation of 100,000 datasets where the true value of \(\theta\) is set (arbitrarily) to 1.75.
set.seed(236)
num.sim <- 100000
n <- 10
theta <- 1.75 # arbitrarily chosen true value
X.obs <- rbeta(n,shape1=theta+1,shape2=1)
y.obs <- sum(log(X.obs))
cat("The observed statistic is ",y.obs,"\n")## The observed statistic is -4.758327X <- runif(n*num.sim) # the null is equivalent to Uniform(0,1)
X <- matrix(X,nrow=num.sim) # each row a dataset of size n
Y <- apply(X,1,function(x){sum(log(x))}) # the simulated statistics
p <- sum(Y>=y.obs)/num.sim # the p-value
cat("The estimated p-value is ",p,"\n")## The estimated p-value is 0.02413We can visualize the empirical sampling distribution using a histogram. See Figure 3.11, in which the \(p\)-value is the “area under the curve” to the right of the observed statistic value (the vertical red line). To ensure that the \(p\)-value estimate is as precise as possible, we should run as many simulations as our computer and our time will allow!
Figure 3.11: The empirical sampling distribution for the statistic \(Y = \sum_{i=1}^n \log X_i\), determined by simulating 100,000 datasets drawn from the distribution \(f_X(x \vert \theta) = \theta x^{\theta-1}\). Here, \(n = 10\) and \(\theta = 1.75\). The observed statistic value, \(y_{\rm obs}\), is indicated by the vertical red line, and the estimated \(p\)-value is the proportion of simulation statistic values falling to the right of the line.
The estimated \(p\)-value is a point estimate. We can add to this estimate by constructing a confidence interval on the unknown true \(p\)-value. We can do this because our simulation is like a binomial experiment, in which
- the number of trials \(k\) is the number of simulations (
num.sim); and - the probability of success \(p\) is the probability of sampling a value of \(Y \geq y_{\rm obs}\) (given that this is an upper-tail test with \(E[Y]\) increasing with \(\theta\)).
In the code below, we denote the observed statistic (here, the number of times we observe \(Y \geq y_{\rm obs}\)) as
u.obs.
f <- function(p,k,u.obs,q)
{
pbinom(u.obs,size=k,prob=p) - q
}
uniroot(f,interval=c(0,1),k=num.sim,u.obs=sum(Y>=y.obs)-1,q=0.975)$root## [1] 0.02320476## [1] 0.02511073(Note how we apply a discreteness correction when computing the lower bound.) Our estimated 95% confidence interval for the true \(p\)-value is [0.0232,0.0251]; we can feel “confident” when we decide, in this situation, to reject the null hypothesis that \(\theta = \theta_o = 1\).
3.8.6 Utilizing Simulations When Data Reduction is Not Possible
The logistic distribution, whose probability density function is \[\begin{align*} f_X(x \vert \mu) = \frac{\exp(\mu-x)}{[1+\exp(\mu-x)]^2} \end{align*}\] for \(x \in (-\infty,\infty)\) and \(\mu \in (-\infty,\infty)\), is not a member of the exponential family of distributions. This means that if we sample \(n\) iid data according to this distribution, we cannot reduce them so as to define a single-number sufficient statistic for \(\mu\). What we can do, however, is the following:
- we can simulate a large number of datasets under the null hypothesis \(\mu = \mu_o\);
- for each dataset, we can record \(\mathcal{L}(\mu_o \vert \mathbf{x})\) and \(\mathcal{L}(\mu_a \vert \mathbf{x})\), and their difference (which is \(\log \lambda_{NP}\)); and
- we can determine the \(\alpha^{\rm th}\) percentile of the distribution of \(\log \lambda_{NP}\) values.
The \(\alpha^{\rm th}\) percentile is \(c'(\alpha) = \log c(\alpha)\), i.e., it is the rejection-region boundary for the most powerful test of the simple hypotheses \(\mu = \mu_o\) and \(\mu = \mu_a\). (However, note that because \(\mu_a\) factors directly into the simulations, what we define is not a uniformly most powerful test, which is to say as we change \(\mu_a\), the value of \(c'(\alpha)\) will also change, unlike the rejection-region boundaries that we derive in single-value sufficient statistic/exponential family distribution contexts.
Below, we show how to carry out simulations to determine the rejection-region boundary, the \(p\)-value, and the test power for a situation in which we sample \(n = 10\) iid data according to a logistic distribution for which \(\mu_o = 1\), with our alternative hypothesis being \(\mu_a = 3\). (See Figure 3.12.)
set.seed(36236)
alpha <- 0.05
num.sim <- 100000
n <- 10
mu.o <- 1
mu.a <- 2
X <- matrix(rlogis(n*num.sim,location=mu.o),nrow=num.sim)
f <- function(x,mu.o)
{
sum(log(dlogis(x,location=mu.o)))
}
log.like.o <- apply(X,1,f,mu.o=mu.o)
log.like.a <- apply(X,1,f,mu.o=mu.a)
delta.log.like <- log.like.o - log.like.a
# The rejection-region boundary
rr <- quantile(delta.log.like,probs=alpha)
cat("The rejection-region boundary is",round(rr,3),"\n")## The rejection-region boundary is -1.362# The p-value for a dataset sampled under the null
X <- rlogis(n,location=mu.o)
delta.log.like.obs <- f(X,mu.o) - f(X,mu.a)
p <- sum(delta.log.like<=delta.log.like.obs)/num.sim
cat("The p-value for the statistic",round(delta.log.like.obs,3),"is",round(p,4),"\n")## The p-value for the statistic 0.834 is 0.3226# The test power for mu = mu.a
X <- matrix(rlogis(n*num.sim,location=mu.a),nrow=num.sim)
log.like.o.p <- apply(X,1,f,mu.o=mu.o)
log.like.a.p <- apply(X,1,f,mu.o=mu.a)
delta.log.like.p <- log.like.o.p - log.like.a.p
power <- sum(delta.log.like.p<rr)/num.sim
cat("The test power for mu =",mu.a,"is",round(power,3),"\n")## The test power for mu = 2 is 0.568
Figure 3.12: The empirical sampling distribution for the statistic \(Y = \log\lambda_{NP}\), determined by simulating 100,000 datasets of size \(n = 10\) drawn from a logistic distribution with mean \(\mu_o = 1\). The estimated rejection-region boundary \(\log c(\alpha)\) is indicated by the vertical red line; if the \(y_{\rm obs} < \log c(\alpha)\) is less than the boundary value, we would reject the null hypothesis that \(\mu_o = 1\).
3.8.7 Large-Sample Tests of the Binomial Success Probability
Earlier in the chapter, we saw that if \[ k > 9\left(\frac{\mbox{max}(p,1-p)}{\mbox{min}(p,1-p)}\right) \,, \] then, given a random variable \(X \sim\) Binomial(\(k\),\(p\)), we can assume \[ X \stackrel{d}{\rightarrow} Y \sim \mathcal{N}(kp,kp(1-p)) \,, \] or that \[ \hat{p} = \hat{p}_{MLE} = \frac{X}{k} \stackrel{d}{\rightarrow} X' \sim \mathcal{N}(p,p(1-p)/k) \,. \] In hypothesis testing, this approximation forms the basis of two different tests: \[\begin{align*} \mbox{Score}~\mbox{Test:} ~~ & \hat{p} \sim \mathcal{N}(p_o,p_o(1-p_o)/k) \\ \mbox{Wald}~\mbox{Test:} ~~ & \hat{p} \sim \mathcal{N}(p_o,\hat{p}(1-\hat{p})/k) \,. \end{align*}\] The only difference between the two is in how the variance is estimated under the null. To carry out these tests, we can simply adapt the expressions for the rejection regions, \(p\)-values, and power given in Chapter 2 for tests of the normal population mean with variance known, with the primary change being the definition of the variance.
We are including the details of the Wald and Score tests here for completeness, in that they are ubiquitous in introductory statistics settings. As they yield only approximate results, we would encourage the reader to always use the exact testing mechanisms described above, while being mindful of the effects of the discreteness of the probability mass function, especially when \(n\) and \(k\) are both small.
3.9 Logistic Regression
In the last chapter, we introduced simple linear regression, in which we model the data-generating process as \[ Y_i = \beta_0 + \beta_1x_i + \epsilon_i \,. \] To perform hypothesis testing (e.g., \(H_o : \beta_1 = 0\) vs. \(H_a : \beta_1 \neq 0\)), we make the assumption that \(\epsilon_i \sim \mathcal{N}(0,\sigma^2)\), or equivalently, that \(Y_i \vert x_i \sim \mathcal{N}(\beta_0+\beta_1x_i,\sigma^2)\). When we make this assumption, we are implicitly stating that the response variable is continuous and that it can take on any value between \(-\infty\) and \(\infty\). But what if this doesn’t actually correctly represent the response variable? Maybe the \(Y_i\)’s are distances with values \(\geq 0\). Maybe each \(Y_i\) belongs to one of several categories, and thus the \(Y_i\)’s are discretely valued. When provided data such as these, it is possible, though not optimal, to utilize simple linear regression. A better choice is to generalize the concept of linear regression, and to utilize this generalization to implement a more appropriate statistical model.
To implement a generalized linear model (or GLM), we need to do two things:
- examine the \(Y_i\) values and select an appropriate distribution for them (discrete or continuous? what is the functional domain?); and
- define a link function \(g(\theta \vert x)\) that maps the line \(\beta_0 + \beta_1 x_i\), which has infinite range, into a more limited range (e.g., \([0,\infty)\)).
Suppose that, in an experiment, the response variable can take on the values “false” and “true.” To generalize linear regression so as to handle these data, we map “false” to 0 and “true” to 1, and assume that we can model the data-generating process using a Bernoulli distribution (i.e., a binomial distribution with \(k = 1\)): \(Y \sim\) Bernoulli(\(p\)). We know that \(0 < p < 1\), so we adopt a link function that maps \(\beta_0 + \beta_1 x\) to the range \((0,1)\). There is no unique choice, but a conventional one is the logit function: \[ g(p \vert x) = \log\left[\frac{p \vert x}{1-p \vert x}\right] = \beta_0 + \beta_1 x ~\implies~ p \vert x = \frac{\exp\left(\beta_0+\beta_1x\right)}{1+\exp\left(\beta_0+\beta_1x\right)} \,. \] Using the logit function to model dichotomous data is dubbed logistic regression. See Figure 3.13.
Figure 3.13: An example of an estimated logistic regression line. The blue line is a sigmoid function; it represents the probability that we would sample a datum of Class 1 as a function of \(x\). The red points are the observed data.
How do we learn a logistic regression model? In linear regression, we can determine values for \(\hat{\beta}_0\) and \(\hat{\beta}_1\) by formulae, the ones we derive when we minimize the sum of squared errors (SSE). For logistic regression, such simple formulae do not exist, and so we estimate \(\beta_0\) and \(\beta_1\) via numerical optimization of the likelihood function \[ \mathcal{L}(\beta_0,\beta_1 \vert \mathbf{y}) = \prod_{i=1}^n p_{Y \vert \beta_0,\beta_1}(y_i \vert \beta_0,\beta_1) = \prod_{i=1}^n p^{y_i}(1-p)^{1-y_i} = p^{\sum_{i=1}^n y_i} (1-p)^{n-\sum_{i=1}^n y_i} \,, \] where \(p_Y(\cdot)\) is the Bernoulli probability mass function. Specifically, we would take the first partial derivatives of \(\mathcal{L}(\beta_0,\beta_1 \vert \mathbf{y})\) with respect to \(\beta_0\) and \(\beta_1\), respectively, set them both to zero (thus allowing us to equate the derivative expressions), and determine the values \(\hat{\beta}_0\) and \(\hat{\beta}_1\) that satisfy the equated derivatives. These are the values at which the bivariate likelihood surface achieves its maximum value. Note that because numerical optimization is an iterative process, logistic regression models are learned more slowly than simple linear regression models.
Let’s step back for a moment. Why would we want to learn a logistic regression model in the first place? After all, it is a relatively inflexible model that might lack the ability to mimic the true behavior of \(p \vert x\). The reason is that because we specify the mathematical form of the model, we can after the fact examine the estimated coefficients and perform inference: we can examine how the response is affected by changes in the predictor variables’ values. This can be important in, e.g., scientific contexts, where explaining how a model works can be as important, if not more important, than its ability to generate accurate and precise predictions. (This is in constrast to commonly used machine learning models, whose mathematical forms cannot be specified a priori and are thus less interpretable after they are learned.)
In simple linear regression, if we increase \(x\) by one unit, we can immediately infer how the response value changes: \[ \hat{Y}' = \hat{\beta}_0 + \hat{\beta}_1 (x + 1) = \hat{\beta}_0 + \hat{\beta}_1 x + \hat{\beta}_1 = \hat{Y} + \hat{\beta}_1 \,. \] For logistic regression, the situation is not as straightforward, because \(p\) changes non-linearly as a function of \(x\). So we fall back on the concept of odds: \[ O(x) = \frac{p(x)}{1-p(x)} = \exp\left(\hat{\beta}_0+\hat{\beta}_1x\right) \,. \] If, e.g., \(O(x) = 4\), then that means that, given \(x\), we are four times more likely to sample a success (1) than a failure (0). How does the odds change if we add one unit to \(x\)? \[ O(x+1) = e^{\hat{\beta}_0+\hat{\beta}_1(x+1)} = \exp\left(\hat{\beta}_0 + \hat{\beta}_1x\right) \times \exp\left(\hat{\beta}_1\right) = O(x) \exp\left(\hat{\beta}_1\right) \,. \] The odds change by a factor of \(\exp\left(\hat{\beta}_1\right)\), which can be greater than or less than one, depending on the sign of \(\hat{\beta}_1\).
It is important to note that when we perform logistic regression, we are simply estimating \(p \vert x\), which is the probability that we would sample a datum belonging to Class 1, given \(x\). How we choose to map \(p \vert x\) to either 0 or 1, if we choose to make that mapping, is not actually part of the logistic regression framework. Classification is a broad topic within statistical learning whose details are beyond the scope of this book. We direct the interested reader to, e.g., Introduction to Statistical Learning by James et al.
3.9.1 Logistic Regression in R
When observed with a telescope, a star is a point-like object, as opposed to a galaxy, which has some angular extent. Telling stars and galaxies apart visually is thus, in relative terms, easy. However, if the galaxy has an inordinately bright core because the supermassive black hole at its center is ingesting matter at a high rate, that core can outshine the rest of the galaxy so much that the galaxy appears to be point-like. Such galaxies with bright cores are dubbed “quasars,” or “quasi-stellar objects,” and they are much harder to tell apart from stars.
Let’s say we are given a dataset showing the difference in magnitude (a logarithmic measure of brightness) at two wavelengths, for 500 stars and 500 quasars. The response variable is a factor variable with two levels, which we dub “Class 0” (here,
QSO) and “Class 1” (STAR). (The mapping of qualitative factors to quantitative levels is by default alphabetical; asSTARcomes afterQSO,STARgets mapped to Class 1. One can always override this default behavior.)
We learn a simple logistic regression model using the
Rfunctionglm(), rather thanlm(), and we specifyfamily=binomial, which means “do logistic regression.” (We can add additional arguments to, e.g., change the link function.)
## [1] "Deviance Residuals"## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -2.646515 -0.894956 0.033093 0.007907 0.843635 3.916292##
## Call:
## glm(formula = class ~ r, family = binomial, data = df)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 23.44801 1.65428 14.17 <2e-16 ***
## r -1.25386 0.08817 -14.22 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1386.3 on 999 degrees of freedom
## Residual deviance: 1040.9 on 998 degrees of freedom
## AIC: 1044.9
##
## Number of Fisher Scoring iterations: 5The
summary()of a learned logistic regression model is similar to that for a linear regression model.
The “deviance residuals,” which show the residuals for each datum, are defined as \[ d_i = \mbox{sign}(Y_i - \hat{Y}_i) \sqrt{-2[Y_i \log \hat{Y}_i + (1-Y_i)\log(1-\hat{Y}_i)]} \,, \] where \[ \hat{Y}_i = \hat{p}_i \vert x_i = \frac{\exp(\hat{\beta}_0+\hat{\beta}_1 x_i)}{1 + \exp(\hat{\beta}_0+\hat{\beta}_1 x_i)} \,. \] The sum of the squared deviance residuals is equal to \(-2 \log \mathcal{L}_{\rm max}\), where \(\mathcal{L}_{\rm max}\) is the maximum value of the joint likelihood of \(\hat{\beta}_0\) and \(\hat{\beta}_1\), given \(\mathbf{x}\). Here, we observe that the deviance residuals are seemingly well-balanced around zero.
The coefficients can be translated to \(y\)-coordinate values as follows: the intercept is \(e^{23.448}/(1+e^{23.448}) \rightarrow 1\) (this is the probability the a sampled datum with
requal to zero is aSTAR), while the odds ratio is \(O_{new}/O_{old} = e^{-1.254}\) (so that every timerincreases by one unit, the probability that a sampled datum is a star is 0.285 times what it had been before: the higher the value ofr, the less and less likely that a sampled datum is actually a star, and the more and more likely that it is a quasar…at least, according to the logistic regression model.
The numbers in the other three columns of the coefficients section are estimated numerically using the behavior of the likelihood function (specifically, the rates at which it curves downward away from the maximum). Some details about how the numbers are calculated are given in an example in the “Covariance and Correlation” section of Chapter 6. It suffices to say here that if we assume that \(\hat{\beta}_0\) and \(\hat{\beta}_1\) are both normally distributed random variables, we reject the null hypothesis that the intercept is 0 (or equivalently \(y = 1/2\)), and that \(\beta_1 = 0\).
The null deviance is \(-2 \log \mathcal{L}_{max,o}\), where \(\mathcal{L}_{max,o}\) is the maximum likelihood when \(\beta_1\) is set to zero. The residual deviance is \(-2 \log \mathcal{L}_{\rm max}\). The difference between these values (here, 1386.3-1040.9 = 345.4), under the null hypothesis that \(\beta_1 = 0\), is assumed to be sampled from a chi-square distribution for 999-998 = 1 degree of freedom. The \(p\)-value is thus
1 - pchisq(345.4,1)or effectively zero: we emphatically reject the null hypothesis that \(\beta_1 = 0\). While this hypothesis test clearly indicates that \(\beta_1\) is not equal to zero, how can we know whether the model itself fits to the data well in an absolute sense? This is a model’s “goodness of fit,” a concept we introduce at the end of this chapter. There is no unique answer to this question in the context of logistic regression; the interested reader should look up, e.g., the Hosmer-Lemeshow statistic. (Note that the test carried out here is analogous to the \(F\)-test in linear regression, and is testing \(H_o: \beta_1 = \beta_2 = \cdots = \beta_p = 0\) versus \(H_a:\) at least one of the \(\beta_i\)’s is non-zero. Because the sampling distribution here is the chi-square distribution as opposed to the normal distribution, the \(p\)-value here will not match the \(p\)-value seen in the coefficients section in general.)
Last, the AIC, or Akaike Information Criterion, is \(-2\) times the model likelihood (or here, the deviance) plus two times the number of variables (here, 2, as the intercept is counted as a variable). Adding the number of variables acts to penalize those models with more variables: the improvement in the maximum likelihood has to be sufficient to justify added model complexity. Discussion of the mathematical details of AIC is beyond the scope of this book; it suffices to say that if we compute it when learning a suite of different models, we would select the model with the smallest value.
We wrap up this example by showing how one would start moving from estimating the Class 1 probabilities for each datum towards predicting classes for each datum. Logistic regression is not in and of itself a “classifier”: it simply outputs probabilities. Naively, we would classify an object with an estimated probability below 0.5 as being an object of Class 0 and one with an estimated probability above 0.5 as being an object of Class 1, but that only works in general if the classes are balanced, i.e., if there are the same number of data of Class 1 as of Class 0. (Here, “works” means “acts to minimize misclassification rates across both classes at the same time.”) If there is class imbalance, then we will almost certainly have to change 0.5 to some other value for optimal classification. In the current example, the classes are balanced, and so putting the “dividing line” at 0.5, as we do in Figure 3.14, is an optimal choice.
Figure 3.14: Boxplots showing the estimated probability that a datum is a star, as a function of the object type (quasar or star). To convert estimated probabilities to predicted classes, one would draw a dividing line between the two boxes: all objects with probabilities below the line would be predicted to be quasars and all others would be predicted to be stars. The line would be placed to, e.g., minimize the number of misclassifications.
3.10 Naive Bayes Regression
The Naive Bayes model is the basis for perhaps the simplest probabilitic classifier, one that is used to, e.g., detect spam emails. The meanings of the words “Naive” and “Bayes” will become more clear below. Note that one would often see this model referred to as the “Naive Bayes classifier.” However, as noted in the last section, there are actually two steps in classification, the first being the estimation of probabilities that a given datum belongs to each class, and the second being the mapping of those probabilities to class predictions. In the last section and here, we are only focusing on the generation of predicted probabilities…hence the title of this section.
(Many would argue that the Naive Bayes model is a machine-learning model. We would argue that it actually is not: the final form of a machine-learning model is unknown before we start the modeling process [e.g., the number of branches that will appear in a classification tree model is unknown and is learned by the machine], whereas with Naive Bayes the mathematical form of the model is fully specified and all we have to do is estimate unknown probabilities. This is akin to the situation with linear regression, where the mathematical form is set and all we have to do is estimate the coefficients…and no one would argue that linear regression is a machine-learning model!)
Let’s assume that we are in a similar setting as the one for logistic regression, but instead of having a response that is a two-level factor variable (i.e., one the represents two classes), the number of levels is \(K \geq 2\). (So instead of just, e.g., “chocolate” and “vanilla” as our response variable values, we can add “strawberry” and other ice cream flavors too!) The ultimate goal of the model is to assign conditional probabilities for each response class, given a datum \(\mathbf{x}\): \(p(C_k \vert \mathbf{x})\), where \(C_k\) denotes “class \(k\).” How do we derive this quantity?
The first step is to apply Bayes’ rule (hence the “Bayes” in “Naive Bayes”): \[ p(C_k \vert \mathbf{x}) = \frac{p(C_k) p(\mathbf{x} \vert C_k)}{p(\mathbf{x})} \,. \] The next step is to expand \(p(\mathbf{x} \vert C_k)\): \[ p(\mathbf{x} \vert C_k) = p(x_1,\ldots,x_p \vert C_k) = p(x_1 \vert x_2,\ldots,x_p,C_k) p(x_2 \vert x_3,\ldots,x_p,C_k) \cdots p(x_p \vert C_k) \,. \] (This is the multiplicative law of probability in action, as applied to a conditional probability. See section 1.4.) The right-most expression above is one that is difficult to evaluate in practice, given all the conditions that must be jointly applied…so this is where the “Naive” aspect of the model comes in. We simplify the expression by assuming (most often incorrectly!) that the predictor variables are all mutually independent, so that \[ p(x_1 \vert x_2,\ldots,x_p,C_k) p(x_2 \vert x_3,\ldots,x_p,C_k) \cdots p(x_p \vert C_k) ~~ \rightarrow ~~ p(x_1 \vert C_k) \cdots p(x_p \vert C_k) \] and thus \[ p(C_k \vert \mathbf{x}) = \frac{p(C_k) \prod_{i=1}^p p(x_i \vert C_k)}{p(\mathbf{x})} \,. \] OK…where do we go from here?
We need to make further assumptions!
- We need to assign “prior probabilities” \(p(C_k)\) to each class. Common choices are \(1/K\) (we view each class as equally probable before we gather data) and \(n_k/n\) (the number of observed data of class \(k\) divided by the overall sample size).
- We also need to assume probability mass and density functions \(p(x_i \vert C_k)\) for each predictor variable (a pmf if \(x_i\) is discrete and a pdf if \(x_i\) is continuous). It is convention to use binomial or multinomial pmfs, depending on the number of levels, with the observed proportions in each level informing the category probability estimate, and normal pdfs, with \(\hat{\mu} = \bar{x_i}\) and \(\hat{\sigma^2} = s_i^2\) (the sample variance).
Ultimately, this model depends on a number of (perhaps unjustified) assumptions. Why would we ever use it? Because the assumption of mutual independence makes model evaluation fast. Naive Bayes is rarely the model underlying the best classifier for any given problem, but when speed is needed (such as in the identification of spam email), one’s choices are limited. (As as general rule: if a model is simple to implement, one should implement it, even if the a priori expectation is that another model will ultimately generate better results. One never knows…)
3.10.1 Naive Bayes Regression With Categorical Predictors
Let’s assume that we have collected the following data:
| \(x_1\) | \(x_2\) | \(Y\) |
|---|---|---|
| Yes | Chocolate | True |
| Yes | Chocolate | False |
| No | Vanilla | True |
| No | Chocolate | True |
| Yes | Vanilla | False |
| No | Chocolate | False |
| No | Vanilla | False |
We learn a Naive Bayes model given these data, in which we assume “False” is Class 0 and “True” is Class 1. If we have a new datum \(\mathbf{x}\) = (“Yes”,“Chocolate”), what is the probability that the response is “True”?
We seek the quantity \[ p(C_1 \vert \mathbf{x}) = \frac{p(C_1) p(\mathbf{x} \vert C_1)}{p(\mathbf{x})} = \frac{p(C_1) p(x_1 \vert C_1) p(x_2 \vert C_1)}{p(x_1,x_2)} \,. \] When we examine the data, we see that \(p(C_1) = 3/7\), as there are three data out of seven with the value \(Y\) = “True.” Now, given \(C_1\), at what rate do we observe “Yes”? (One time out of three…so \(p(x_1 \vert C_1) = 1/3\).) What about “Chocolate”? (Two times out of three…so \(p(x_2 \vert C_1) = 2/3\).) The numerator is thus \(3/7 \times 1/3 \times 2/3 = 2/21\). The value of the denominator, \(p(x_1,x_2)\), is determined utilizing the Law of Total Probability: \[\begin{align*} p(x_1,x_2) &= p(x_1 \vert C_1) p(x_2 \vert C_1) p(C_1) + p(x_1 \vert C_2) p(x_2 \vert C_2) p(C_2) \\ &= 2/21 + 2/4 \times 2/4 \times 4/7 = 2/21 + 4/28 = 2/21 + 3/21 = 5/21 \,. \end{align*}\] And so now we know that \[ p(\mbox{True} \vert \mbox{Yes,Chocolate}) = \frac{2/21}{5/21} = \frac{2}{5} \,. \]
3.10.2 Naive Bayes Regression With Continuous Predictors
Let’s assume we have the following data regarding credit-card defaults, where \(x\) represents the credit-card balance and \(Y\) is a categorical variable indicating whether a default has occurred:
| \(x\) | 1487.00 | 324.74 | 988.21 | 836.30 | 2205.80 | 927.89 | 712.28 | 706.16 | 1774.69 |
|---|---|---|---|---|---|---|---|---|---|
| \(Y\) | Yes | No | No | No | Yes | No | No | No | Yes |
Let’s now suppose someone came along with a credit balance of $1,200. According to the Naive Bayes model, given this balance, what is the probability of a credit default?
The Naive Bayes model in this particular case is \[ p(Y \vert x) = \frac{p(x \vert Y) p(Y)}{p(x \vert Y) p(Y) + p(x \vert N) p(N)} \,, \] where we can observe immediately that \(p(Y) = 3/9 = 1/3\) and \(p(N) = 6/9 = 2/3\). To compute, e.g., \(p(x \vert Y)\), we first compute the sample mean and sample standard deviation for the observed data for which \(Y\) is “Yes”:
## [1] 1822.5## [1] 361.78The mean is $1,822.50 and the standard deviation is $361.78, so the probability density associated with observing $1,200 is
## [1] 0.0002509367The density is 2.51 \(\times\) 10\(^{-4}\). As far as for those data for which \(Y\) is “No”:
## [1] 0.0002748351The density is 2.75 \(\times\) 10\(^{-4}\). Thus \[ p(Y \vert x) = \frac{2.51 \cdot 0.333}{2.51 \cdot 0.333 + 2.75 \cdot 0.667} = \frac{0.834}{0.834 + 1.834} = 0.313 \,. \] We would predict that there is roughly a 1 in 3 chance that a person with a credit balance of $1,200 will default on their debt.
3.10.3 Naive Bayes Applied to Star-Quasar Data
Here, we learn a Naive Bayes model that we can use to differentiate between stars and quasars, utilizing functions from
R’se1071package.
##
## Naive Bayes Classifier for Discrete Predictors
##
## Call:
## naiveBayes.default(x = X, y = Y, laplace = laplace)
##
## A-priori probabilities:
## Y
## QSO STAR
## 0.5 0.5
##
## Conditional probabilities:
## r
## Y [,1] [,2]
## QSO 19.35770 0.8282726
## STAR 17.96389 1.3651572The summary of the model shows that the classes are balanced (as the
A-priori probabilitiesare 0.5 for each class). It then shows the estimated distributions ofrvalues for quasars (a normal with estimated mean 19.358 and standard deviation 0.828) and stars (mean 17.964 and standard deviation 1.365). See Figure 3.15.
Figure 3.15: An illustration of the Naive Bayes regression model, as applied to the star-quasar dataset. The red curve is the estimated normal probability density function for stars, while the green curve is the estimated pdf for quasars. Because the two classes in this example are balanced, we can state that where the amplitude of the red curve is higher, the predicted class would be STAR; otherwise, it would be QUASAR.
3.11 The Beta Distribution
The beta distribution is a continuous distribution that is commonly used to model random variables with finite, bounded domains. Its probability density function is given by \[ f_X(x) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}\,, \] where \(x \in [0,1]\), \(\alpha\) and \(\beta\) are both \(> 0\), and the normalization constant \(B(\alpha,\beta)\) is \[ B(\alpha,\beta) = \int_0^1 x^{\alpha-1}(1-x)^{\beta-1} dx = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)} \,. \] (See Figure 3.16.) We have seen the gamma function, \(\Gamma(\alpha)\), before; it is defined as \[ \Gamma(\alpha) = \int_0^\infty x^{\alpha-1} e^{-x} dx \,. \] There are two things to note about the gamma function. The first is its recursive property: \(\Gamma(\alpha+1) = \alpha \Gamma(\alpha)\). (This can be shown by applying integration by parts.) The second is that when \(\alpha\) is a positive integer, the gamma function takes on the value \((\alpha-1)! = (\alpha-1)(\alpha-2) \cdots 1\). (Note that \(\Gamma(1) = 0! = 1\).)
Regarding the statement above about “model[ing] random variables with finite, bounded domains”: if a set of \(n\) iid random variables \(\mathbf{X}\) has domain \([a,b]\), we can define a new set of random variables \(\mathbf{Y}\) via the transformation \[ \mathbf{Y} = \frac{\mathbf{X}-a}{b-a} \] such that the domain becomes \([0,1]\). We can model these newly defined data with the beta distribution. (Note the word can: we can model these data with the beta distribution, but we don’t have to, and it may be the case that there is another distribution bounded on the interval \([0,1]\) that ultimately better describes the data-generating process. The beta distribution just happens to be commonly used.)
But…in the end, what does this all have to do with the binomial distribution, the subject of this chapter? We know the binomial has a parameter \(p \in [0,1]\) and the domain of the beta distribution is \([0,1]\), but is there more? Let’s write down the binomial pmf: \[ \binom{k}{x} p^x (1-p)^{k-x} = \frac{k!}{x!(k-x)!} p^x (1-p)^{k-x} \,. \] This pmf dictates the probability of observing a particular value of \(x\) given \(k\) and \(p\). But what if we turn this around a bit…and examine this function if we fix \(k\) and \(x\) and vary \(p\) instead? In other words, let’s examine the likelihood function \[ \mathcal{L}(p \vert k,x) = \frac{k!}{x!(k-x)!} p^x (1-p)^{k-x} \,. \] We can see immediately that the likelihood has the form of a beta distribution if we set \(\alpha = x+1\) and \(\beta = k-x+1\): \[ \mathcal{L}(p \vert k,x) = \frac{\Gamma(\alpha+\beta-1)}{\Gamma(\alpha)\Gamma(\beta)} p^{\alpha-1} (1-p)^{\beta-1} \,, \] except that the normalization term is not quite right: here we have \(\Gamma(\alpha+\beta-1)\) instead of \(\Gamma(\alpha+\beta)\). But that’s fine: there is no requirement that a likelihood function integrate to one over its domain. (Here, as the interested reader can verify, the likelihood function integrates to \(1/(k+1)\).) So, in the end, if we observe a random variable \(X \sim\) Binomial(\(k,p\)), then the likelihood function \(\mathcal{L}(p \vert k,x)\) has the shape (if not the normalization) of a Beta(\(x+1,k-x+1\)) distribution.
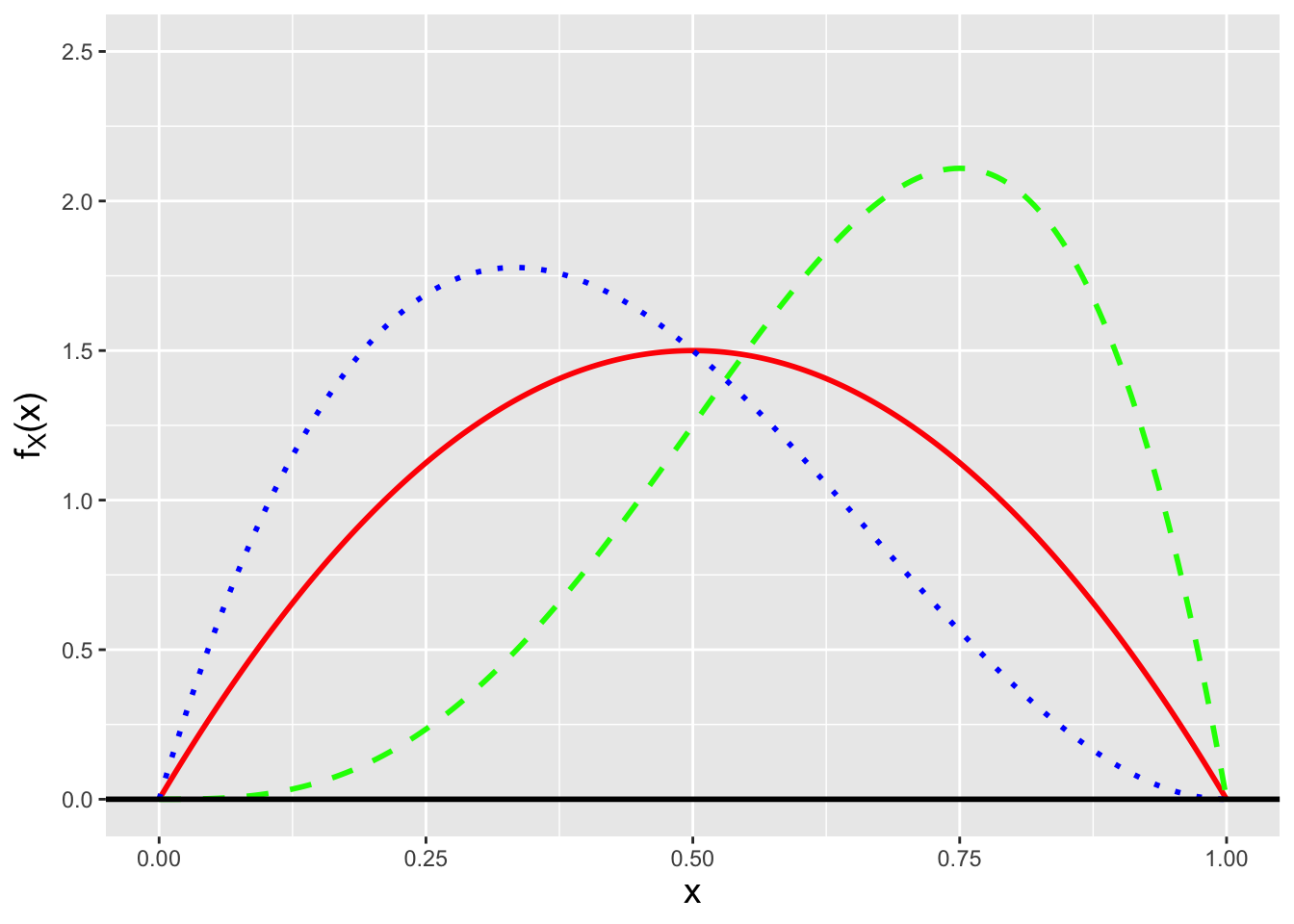
Figure 3.16: Three examples of beta probability density functions: Beta(2,2) (solid red line), Beta(4,2) (dashed green line), and Beta(2,3) (dotted blue line).
3.11.1 The Expected Value of a Beta Random Variable
The expected value of a random variable sampled from a Beta(\(\alpha,\beta\)) distribution is \[\begin{align*} E[X] = \int_0^1 x f_X(x) dx &= \int_0^1 x \frac{x^{\alpha-1} (1-x)^{\beta-1}}{B(\alpha,\beta)} dx \\ &= \int_0^1 \frac{x^{\alpha} (1-x)^{\beta-1}}{B(\alpha,\beta)} dx \\ &= \int_0^1 \frac{x^{\alpha} (1-x)^{\beta-1}}{B(\alpha+1,\beta)} \frac{B(\alpha+1,\beta)}{B(\alpha,\beta)} dx \\ &= \frac{B(\alpha+1,\beta)}{B(\alpha,\beta)} \int_0^1 \frac{x^{\alpha} (1-x)^{\beta-1}}{B(\alpha+1,\beta)} dx \\ &= \frac{B(\alpha+1,\beta)}{B(\alpha,\beta)} \,. \end{align*}\] The last result follows from the fact that the integrand is the pdf for a Beta(\(\alpha+1,\beta\)) distribution, and the integral is over the entire domain, hence the integral evaluates to 1.
Continuing, \[\begin{align*} E[X] &= \frac{B(\alpha+1,\beta)}{B(\alpha,\beta)} \\ &= \frac{\Gamma(\alpha+1) \Gamma(\beta)}{\Gamma(\alpha+\beta+1)} \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} \\ &= \frac{\alpha \Gamma(\alpha)}{(\alpha+\beta)\Gamma(\alpha+\beta)} \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)} \\ &= \frac{\alpha}{\alpha+\beta} \,. \end{align*}\] Here, we take advantage of the recursive property of the gamma function.
We can utilize a similar strategy to determine the variance of a beta random variable, starting by computing \(E[X^2]\) and utilizing the shortcut formula \(V[X] = E[X]^2 - (E[X])^2\). The final result is \[ V[X] = \frac{\alpha \beta}{(\alpha+\beta)^2(\alpha+\beta+1)} \,. \]
3.11.2 The Sample Median of a Uniform(0,1) Distribution
The Uniform(0,1) distribution is \[ f_X(x) = 1 ~~~ x \in [0,1] \,. \] Let’s assume that we draw \(n\) iid data from this distribution, with \(n\) odd. Then we can utilize a result from order statistics to write down the pdf of the sample median, which is the \(j^{\rm th}\) order statstic (where \(j = (n+1)/2\)): \[ f_{((n+1)/2)}(x) = \frac{n!}{\left(\frac{n-1}{2}\right)! \left(\frac{n-1}{2}\right)!} f_X(x) \left[ F_X(x) \right]^{(n-1)/2} \left[ 1 - F_X(x) \right]^{(n-1)/2} \,. \] Given that \[ F_X(x) = \int_0^x dy = x ~~~ x \in [0,1] \,, \] we can write \[ f_{((n+1)/2)}(x) = \frac{n!}{\left(\frac{n-1}{2}\right)! \left(\frac{n-1}{2}\right)!} x^{(n-1)/2} (1-x)^{(n-1)/2} \,, \] for \(x \in [0,1]\). This function has both the form of a beta distribution (with \(\alpha = \beta = (n+1)/2\)) and the domain of a beta distribution, so \(\tilde{X} \sim\) Beta\(\left(\frac{n+1}{2},\frac{n+1}{2}\right)\).
(In fact, we can go further and state a more general result: \(X_{(j)} \sim\) Beta(\(j,n-j+1\)): all the order statistics for data drawn from a Uniform(0,1) distribution are beta-distributed random variables! See Figure 3.17.)
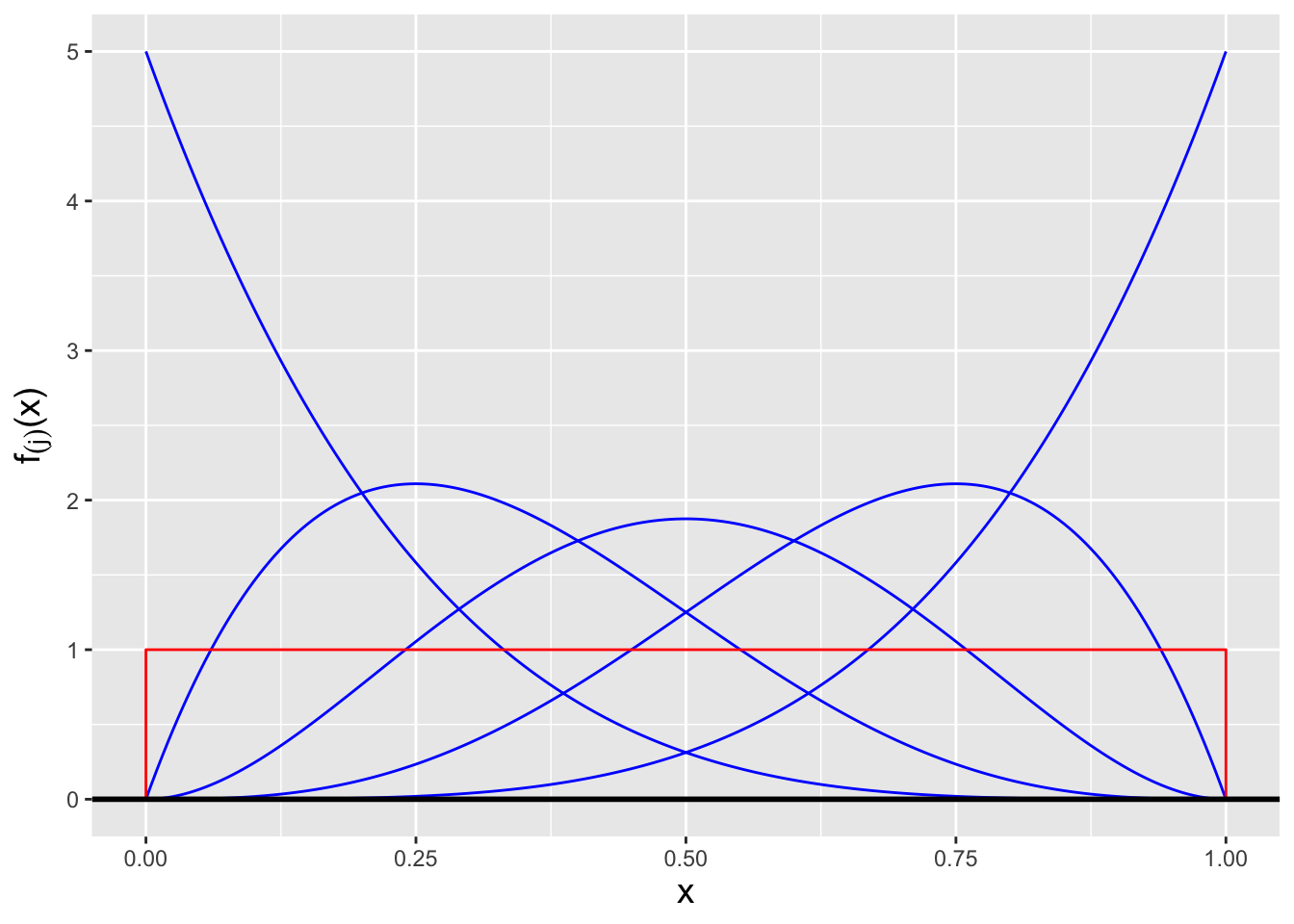
Figure 3.17: The order statistic probability density functions \(f_{(j)}(x)\) for, from left to right, \(j = 1\) through \(j = 5\), for the situation in which \(n = 5\) iid data are drawn from a Uniform(0,1) distribution (overlaid in red). Each pdf is itself a beta distribution, with parameter values \(j\) and \(n-j+1\).
3.12 The Multinomial Distribution
Let’s suppose we are in a situation in which we are gathering categorical data. For instance, we might be
- throwing a ball and recording which of bins numbered 1 through \(m\) it lands in;
- categorizing the condition of old coins as “mint,” “very good,” “fine,” etc.; or
- classifying a galaxy as being a spiral galaxy, an elliptical galaxy, or an irregular galaxy.
These are examples of multinomial trials, which is a generalization of the concept of binomial trials to situations where the number of possible outcomes is \(m > 2\) rather than \(m = 2\). Earlier in this chapter, we wrote down the five properties of binomial trials. The analogous properties of a multinomial experiment are the following.
- It consists of \(k\) trials, with \(k\) chosen in advance.
- There are \(m\) possible outcomes for each trial.
- A trial may have no more than one realized outcome.
- The outcomes of each trial are independent.
- The probability of achieving the \(i^{th}\) outcome is \(p_i\), a constant quantity.
- The probabilities of each outcome sum to one: \(\sum_{i=1}^m p_i = 1\).
- The number of trials that achieve a particular outcome is \(X_i\), with \(\sum_{i=1}^m X_i = k\).
The probability of any given outcome \(\{X_1,\ldots,X_m\}\) is given by the multinomial probability mass function: \[ p(x_1,\ldots,x_m \vert p_1,\ldots,p_m) = \frac{k!}{x_1! \cdots x_m!}p_1^{x_1}\cdots p_m^{x_m} \,. \] The distribution for any given \(X_i\) itself is binomial, with \(E[X_i] = kp_i\) and \(V[X_i] = kp_i(1-p_i)\). This makes intuitive sense, as one either observes \(i\) as a trial outcome (success), or something else (failure). However, the \(X_i\)’s are not independent random variables; the covariance between \(X_i\) and \(X_j\), a metric of linear dependence, is Cov(\(X_i\),\(X_j\)) = \(-kp_ip_j\) if \(i \neq j\). (We will discuss the concept of covariance in Chapter 6.) This also makes intuitive sense: given that the number of trials \(k\) is fixed, observing more data that achieve one outcome will usually mean we will observe fewer data achieving any other given outcome.
For our immediate purposes, the context in which we work with the multinomial distribution is hypothesis testing.
A single multinomial experiment yields a single data vector \(\mathbf{X} = \{X_1,\ldots,X_m\}\). This vector is trivially a sufficient statistic for the vector of probabilities \(\mathbf{p} = \{p_1,\ldots,p_m\}\), and the probability mass function of the sampling distribution for this statistic is simply the multinomial pmf given above. Because we are dealing with a multivariate distribution, we cannot easily determine hypothesis test \(p\)-values by hand; rather, we fall back on the definition that a \(p\)-value is the probability of observing the statistic value we see or a value that is more extreme, and state that the \(p\)-value for a multinomial test is the probability that a data vector simulated under the null hypothesis has a pmf value that is smaller than the observed pmf value. Estimating the \(p\)-value for a multinomial test is easily done, as we show in the example below.
3.12.1 Performing a Multinomial Test
Imagine that we are scientists, sitting on a platform in the middle of a plain. We are recording the number of animals of a particular species that we see, and the azimuthal angle for each one. (An azimuthal angle is, e.g., \(0^\circ\) when looking directly north, and 90\(^\circ\), 180\(^\circ\), and 270\(^\circ\) as we look east, south, and west, etc.) The data we observe are
| angle range | 0\(^\circ\)-90\(^\circ\) | 90\(^\circ\)-180\(^\circ\) | 180\(^\circ\)-270\(^\circ\) | 270\(^\circ\)-360\(^\circ\) |
|---|---|---|---|---|
| number of animals | 28 | 32 | 17 | 23 |
and the question we wish to answer is whether the animals uniformly distributed as a function of angle.
To answer this question, we simulate \(100{,}000\) data vectors given the null hypothesis \(H_o : \{p_1 = 0.25, p_2 = 0.25, p_3 = 0.25, p_4 = 0.25\}\) and determine the proportion of vectors with multinomial pmf values that are smaller than the value we observe:
O <- c(28,32,17,23)
p <- rep(1/4,4)
pmf.obs <- dmultinom(O,prob=p) # the observed multinomial pmf value
set.seed(101)
num.sim <- 100000
k <- sum(O)
m <- length(O)
X <- rmultinom(num.sim,k,p) # generates an m x num.sim matrix
# (m determined as the length of p)
pmf <- apply(X,2,function(x){dmultinom(x,prob=p)}) # pmf vector
sum(pmf<pmf.obs)/num.sim## [1] 0.15974What does
apply()do? It calls the function given as the third argument (which evaluates the multinomial probability mass function given a set of four data \(\mathbf{x}\) and a a set of four probabilities \(\mathbf{p}\)) to each column (hence the “2” as the second argument…“1” would denote rows) of the matrix \(\mathbf{X}\). It is a convenient function that allows us to not have to embed the evaluation of the multinomial pmf into aforloop that would iterate over all the rows of the matrix. We note that the above computation takes $$1 CPU second on a standard desktop/laptop computer.
We observe \(p = 0.160\), i.e., approximately \(16{,}000\) of the \(100{,}000\) simulated data vectors have pmf values smaller than what we observe. We thus fail to reject the null hypothesis and conclude that it is plausible that the animals are distributed uniformly as a function of angle.
The multinomial hypothesis test is exact, in the sense that the data are distributed according to the multinomial distribution, but because we only sample a finite number of data vectors, the \(p\)-value is an estimate and not an exact value. We can utilize the framework given earlier in the chapter for constructing confidence intervals for the binomial probability \(p\) to ascertain the level of uncertainty in the estimated \(p\)-value:
y.obs <- sum(pmf<pmf.obs)
f <- function(p,k,y.obs,q)
{
pbinom(y.obs,size=k,prob=p) - q
}
uniroot(f,interval=c(0,1),k=num.sim,y.obs=y.obs-1,q=0.975)$root## [1] 0.1574441## [1] 0.1620439The 95% two-sided confidence interval on the true \(p\)-value is \([0.1574,0.1620]\). To decrease the interval length, we simply increase
num.sim, with the tradeoff that the computation time becomes that much longer.
3.13 Chi-Square-Based Hypothesis Testing
Performing a hypothesis test that utilizes the multinomial distribution is essentially impossible to do by hand; multinomial distributions are intrinsically high-dimensional and the data (the numbers of counts in each bin) are not iid. Thus in the era before computers, statisticians could not carry out exact hypothesis tests. In a paper published in 1900, the statistician Karl Pearson noted that as \(k \rightarrow \infty\), multinomial random variables converge in distribution to multivariate normal random variables (with the latter being something we will discuss in Chapter 6), and that the statistic \[ W = \sum_{i=1}^m \frac{(X_i-E[X_i])^2}{E[X_i]} = \sum_{i=1}^m \frac{(X_i - kp_i)^2}{kp_i} \] converges in distribution to a chi-square random variable for \(m-1\) degrees of freedom. (We subtract 1 because only \(m-1\) of the multinomial probabilities can freely vary; the \(m^{th}\) one is constrained by the fact that the probabilities must sum to 1. This constraint is what makes multinomial data not iid.)
The computation of the test statistic \(W\) is the basis of the chi-square goodness-of-fit test, or chi-square GoF test. For this test,
- we reject the null hypothesis if \(W > w_{RR}\);
- the rejection region boundary is \(w_{RR} = F_{W(m-1)}^{-1}(1-\alpha)\) (in
R,qchisq(1-alpha,m-1)); - the \(p\)-value is \(1 - F_{W(m-1)}(w_{\rm obs})\) (e.g.,
1-pchisq(w.obs,m-1)); and - by convention, \(kp_i\) must be \(\geq\) 5 in each bin for the test to yield a valid result.
At this point, we should state that one should always implement exact multinomial tests rather than chi-square GoF tests, given the choice. We are discussing the chi-square GoF test here because its use is ubiquitous in statistics and thus every student should know what it is and how it is carried out…but not because one should actually use it now, in the age of computers. The price that we pay when we use the chi-square GoF test is that, for relatively small values of \(k\), it yields biased \(p\)-value estimates. In an example below, we demonstrate that the chi-square GoF test yields \(p\)-values that are, on average, smaller than expected, making it less conservative than the exact multinomial test (i.e., it rejects correct null hypotheses at a higher rate than we would expect).
There are two variations on the chi-square GoF test for which no exact analogues exist, ones in which the inputs are tables of observed data. The tests differ depending upon how we collect data:
- chi-square test of independence: the question is whether two variables are associated with each other in a population; subjects are selected and the values of two variables are recorded for each. For instance, we might select \(k\) people at random and record whether or not they have had Covid-19, and also record whether or not they initially had zero, one, or two vaccine shots, and put these data into a table with, e.g., “yes” and “no” defining the rows and 0, 1, and 2 defining the columns. If we reject the null, we are stating that the distributions of data along, e.g., each row are statistically significantly different from each other.
- chi-square test of homogeneity: the question is whether the distribution of a single variable is the same for two subgroups of a population, with subjects being selected randomly from each subgroup separately. For instance, we might select \(k\) people under 20 years of age and ask if they prefer vanilla, chocolate, or strawberry ice cream, and then repeat the process for people of age 20 or over, and put the data into a table similar to that described for the test of independence above.
Whether we perform a test of independence versus one of homogeneity affects the interpretation of results, but algorithmically the tests are identical. Under the null hypothesis, \[ \widehat{E[X_{ij}]} = \frac{r_i c_j}{k} \,, \] i.e., the expected value in the cell in row \(i\) and column \(j\) is the product of the total number of data in row \(i\) and column \(j\), divided by the total number of data overall. Then, \[ W = \sum_{i=1}^r \sum_{j=1}^c \frac{(X_{ij} - \widehat{E[X_{ij}]})^2}{\widehat{E[X_{ij}]}} \mathrel{\dot\sim} \chi_{(r-1)(c-1)}^2 \,, \] i.e., the test statistic \(W\) is, under the null, assumed to be chi-square distributed for \((r-1) \times (c-1)\) degrees of freedom. (Because we do not specify exact probabilities for observing data in each table cell under the null, the observed data are not sampled according to a multinomial distribution…and, in fact, we cannot specify an exact distribution. Hence for testing independence and homogeneity given categorical data, the chi-square framework is going to be the most appropriate framework for us to use.)
3.13.1 Chi-Square Goodness of Fit Test
Let’s go back to working with our animal/angle data, and determine, via the use of the chi-square GoF test, whether it is plausible that the number of animals is distributed uniformly as a function of angle.
We first compute the test statistic: \[\begin{align*} W &= \sum_{i=1}^m \frac{(X_i - kp_i)^2}{kp_i} = \frac{(28-25)^2}{25} + \frac{(32-25)^2}{25} + \frac{(17-25)^2}{25} + \frac{(23-25)^2}{25} \\ &= \frac{9}{25} + \frac{49}{25} + \frac{64}{25} + \frac{4}{25} = \frac{126}{25} = 5.04 \,. \end{align*}\] The number of degrees of freedom is \(m-1 = 3\), so the rejection region boundary is \(F_{W}^{-1}(1-\alpha)\) =
qchisq(0.95,3)= 7.815. Since 5.04 \(<\) 7.815, we fail to reject the null hypothesis that the animals are distributed uniformly as a function of azimuthal angle. See Figure 3.18.
Figure 3.18: An illustration of the sampling distribution and rejection region for the chi-square goodness-of-fit test. Here, the number of degrees of freedom is 3, so the rejection region are values of chi-square above 7.815. The observed test statistic is 5.04, which lies outside the rejection region, hence we fail to reject the null hypothesis.
The observed \(p\)-value is
1 - pchisq(5.04,3)= 0.169, which is 5.6% larger than the value observed for the exact multinomial test (0.160, with 95% CI \([0.1574,0.1620]\) for \(100{,}000\) simulations). As we will see below, sometimes the \(p\)-value is larger and sometimes smaller, but on average the \(p\)-value observed for the chi-square GoF test will be smaller than that observed for the multinomial test, at least for small values of \(k\).
3.13.2 The Average p-Value Difference Between the Multinomial and Chi-Square GoF Tests
Let’s suppose that in an experiment, we toss a six-sided die \(k\) times and record the result. For instance, we might toss it \(k = 10\) times, and record the data vector \(\mathbf{X} = \{2,1,3,1,0,3\}\) (i.e., we observe 1 two times, 2 one time, etc.). We wish to test the hypothesis that the die is fair. On average, what is the difference in the \(p\)-value observed when utilize the exact multinomial test versus when we utilize the approximate chi-square GoF test?
Let’s first illustrate how we would determine the average difference when \(k = 30\). (See Figure 3.19.) For this number of trials, the expected number of counts in each bin is exactly 5, i.e., this is the minimum number of trials required by convention when carrying out the chi-square GoF test.
k <- 30
m <- 6
p <- rep(1/m,m)
set.seed(101)
num.rep <- 1000
p.chi <- rep(NA,num.rep)
p.mult <- rep(NA,num.rep)
delta.p <- rep(NA,num.rep)
num.sim <- 1000
for ( ii in 1:num.rep ) {
X.obs <- rmultinom(1,k,p)
W <- sum((X.obs-k*p)^2/(k*p))
p.chi[ii] <- 1 - pchisq(W,m-1)
obs <- dmultinom(X.obs,prob=p)
X <- rmultinom(num.sim,k,p)
a <- apply(X,2,function(x,p){dmultinom(x,prob=p)},p=p)
p.mult[ii] <- sum(a<=obs)/num.sim
delta.p[ii] <- p.mult[ii] - p.chi[ii]
}
cat("Mean Difference:",round(mean(delta.p),5),"\n")## Mean Difference: 0.0098## SE Difference: 0.00135ggplot(data=data.frame(delta.p),mapping=aes(x=delta.p,y=after_stat(density))) +
geom_histogram(fill="dodgerblue",bins=25) +
geom_vline(xintercept=0,col="seagreen",lty=2) +
xlab(expression(Delta*"p")) +
base_theme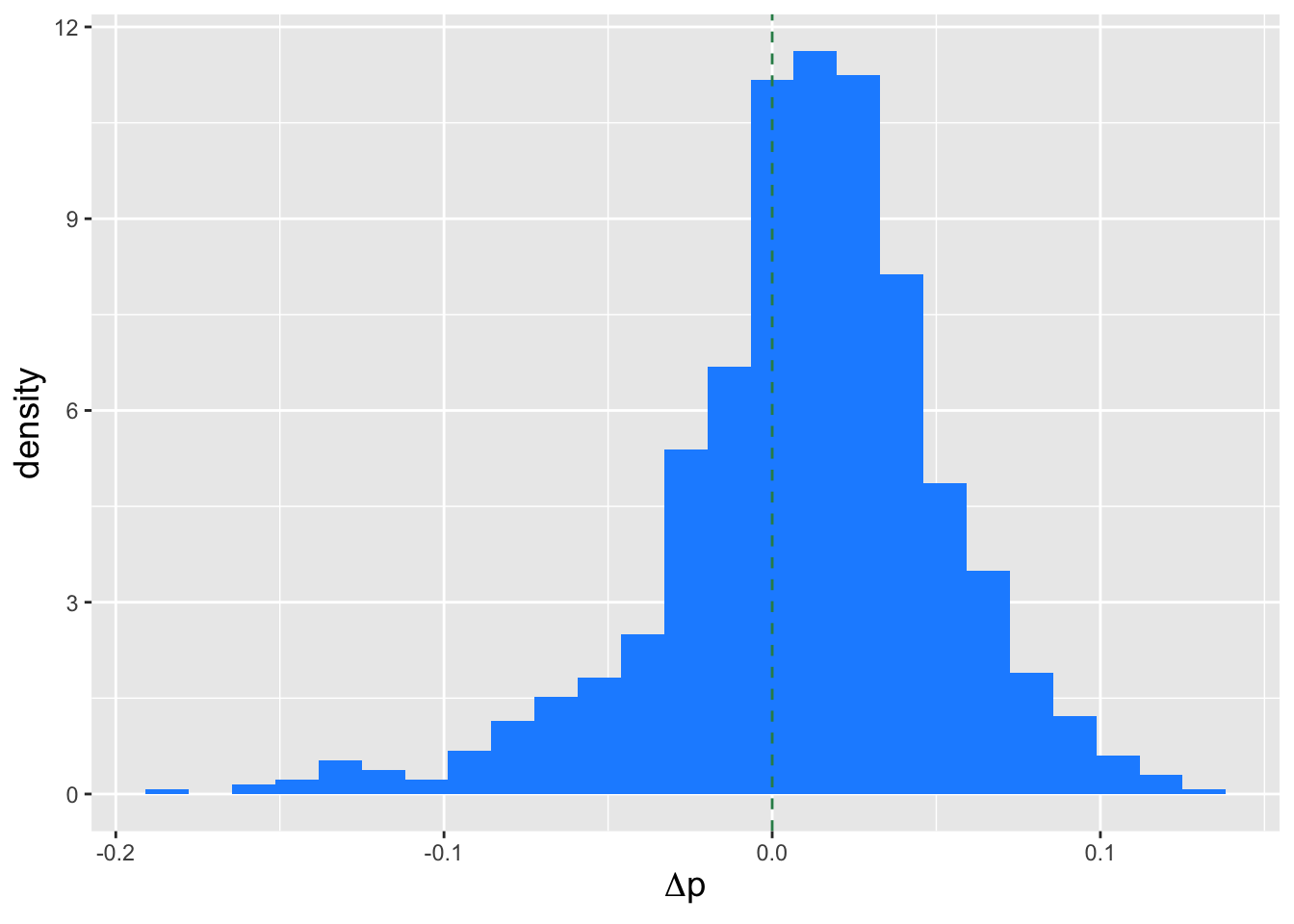
Figure 3.19: Histogram showing the empirical distribution of values of \(\Delta p = p_{\rm mult} - p_{\rm chi}\) that arise when we repeatedly toss a die 30 times and test whether the die is fair. If \(\Delta p > 0\), then the chi-square test is less conservative, i.e., we are more likely to reject a correct null than if we are to use the exact multinomial test. Here, the average value of \(\Delta p\) is \(\approx 0.01\).
We find that for \(k = 30\), the average value of \(\Delta p = p_{\rm mult} - p_{\rm chi}\) is \(\approx 0.01\), i.e., on average the chi-square GoF test is less conservative (or more likely to result in the rejection of a correct null hypothesis).
In Figure 3.20, we show how the average value of \(\Delta p\) changes as a function of \(k\). We see here that while by convention the expected number of counts per bin is supposed to be at least five, it is only when the expected counts reach \(\approx\) 20 or more that we no longer observed a statistically significant difference between the average \(p\)-values.
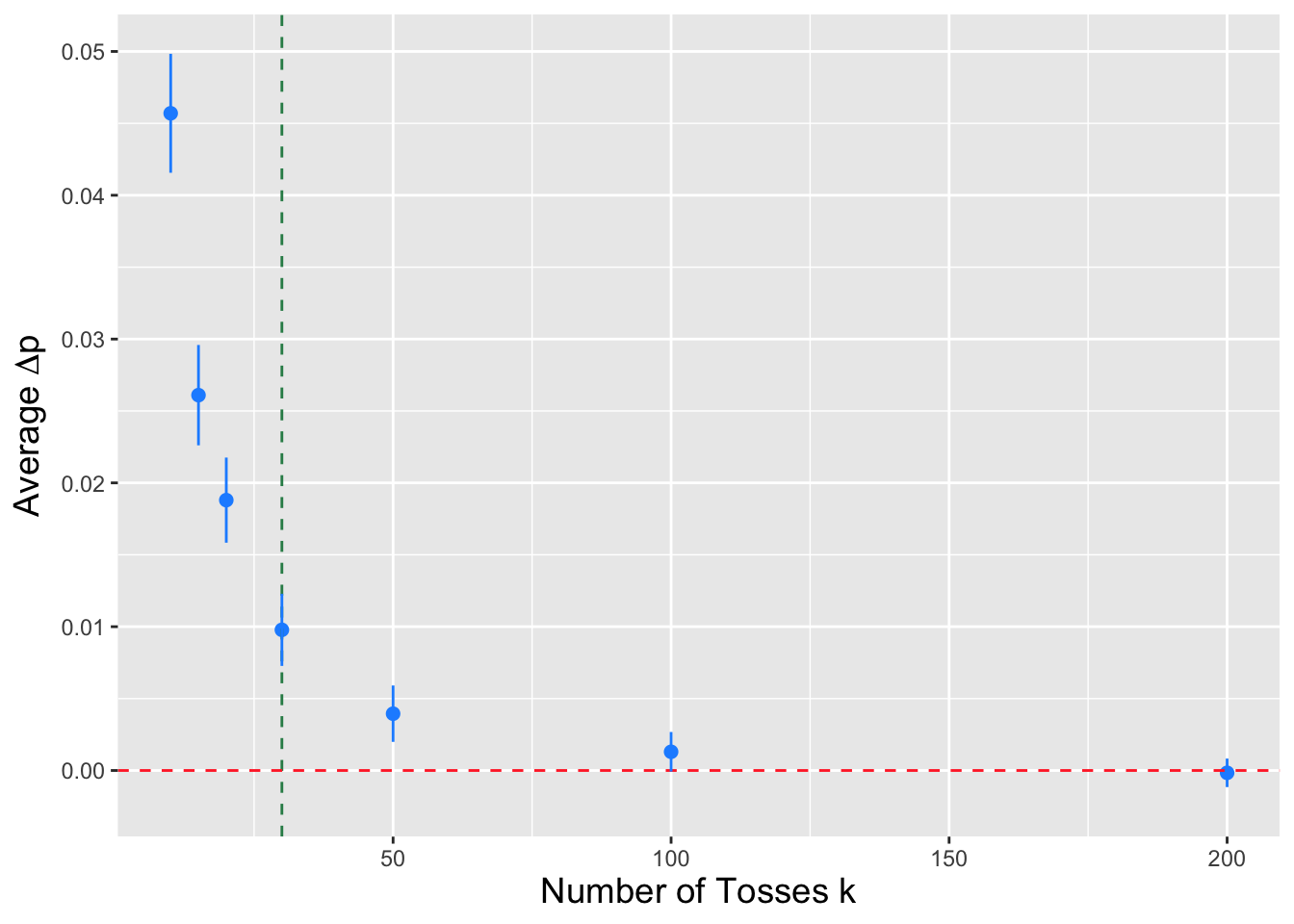
Figure 3.20: The average value of \(\Delta p = p_{\rm mult} - p_{\rm chi}\) as a function of the number of tosses of a six-sided die. The vertical dashed green line at \(k = 30\) represents where the expected number of counts in each data bin is exactly 5, the minimum value conventionally required for use of the chi-square GoF test.
3.13.3 Chi-Square Test of Independence
Let’s go back to our animal data. When we observe the animals in each quadrant, let’s suppose we also record their colors: black or red. So now are data look like this:
| 0\(^\circ\)-90\(^\circ\) | 90\(^\circ\)-180\(^\circ\) | 180\(^\circ\)-270\(^\circ\) | 270\(^\circ\)-360\(^\circ\) | ||
|---|---|---|---|---|---|
| black | 20 | 18 | 5 | 14 | 57 |
| red | 8 | 14 | 12 | 9 | 43 |
| 28 | 32 | 17 | 23 |
When we record two attributes for each subject (here, azimuthal angle and color), we can perform a chi-square test of independence to answer the question of whether the attributes are independent random variables. In other words, here, does the coloration depend on angle? The null hypothesis is no. We will test this hypothesis assuming \(\alpha = 0.05\).
We first determine the expected number of counts in each bin, \(\widehat{E[X_{ij}]} = r_i c_j / k\):
| 0\(^\circ\)-90\(^\circ\) | 90\(^\circ\)-180\(^\circ\) | 180\(^\circ\)-270\(^\circ\) | 270\(^\circ\)-360\(^\circ\) | ||
|---|---|---|---|---|---|
| black | 57 \(\cdot\) 28/100 = 15.96 | 57 \(\cdot\) 32/100 = 18.24 | 57 \(\cdot\) 17/100 = 9.69 | 57 \(\cdot\) 23/100 = 13.11 | 57 |
| red | 43 \(\cdot\) 28/100 = 12.04 | 43 \(\cdot\) 32/100 = 13.76 | 43 \(\cdot\) 17/100 = 7.31 | 43 \(\cdot\) 23/100 = 9.89 | 43 |
| 28 | 32 | 17 | 23 |
We can already see that working with the numbers directly is tedious. Can we make a matrix of such numbers using
R?
r <- c(57,43)
c <- c(28,32,17,23)
E <- (r %*% t(c))/sum(r) # multiply r and the transpose of c
print(E) # much better## [,1] [,2] [,3] [,4]
## [1,] 15.96 18.24 9.69 13.11
## [2,] 12.04 13.76 7.31 9.89If we wish to continue using
R, we need to define a matrix of observed data values:
## [,1] [,2] [,3] [,4]
## [1,] 20 18 5 14
## [2,] 8 14 12 9Now we have what we need. The test statistic is
## [1] 7.805and the number of degrees of freedom is \((r-1)(c-1) = 1 \cdot 3 = 3\), so the rejection region boundary is
## [1] 7.815We find that if \(\alpha = 0.05\), we cannot reject the null hypothesis. We might be tempted to do so, as our test statistic very nearly falls into the rejection region, but we cannot. We could, if we were so inclined, remind ourselves that chi-square-based hypothesis tests are approximate, and run a simulation to try to estimate the true distribution of \(W\), and see what the rejection region and \(p\)-value actually are…that way, we might be able to actually reject the null. But really, at the end of the day, such a result should simply motivate us to gather more data!
3.14 Exercises
Let \(X_1,...,X_n\) be \(n\) data drawn from a \(\mathcal{N}(2,4)\) distribution. Write down the probability that exactly \(m\) of the \(n\) data have values \(> 2\).
You are a habitual buyer of raffle tickets. Each ticket costs $1, and each time you buy a ticket, you have a 40% chance of having a winning ticket, for which you will receive $3. You decide to keep buying tickets until you win for the first time. Let the random variable \(F\) denote the total number of losing tickets that you buy, and let \(W\) denote the total amount of money you win (or lose!). (a) \(F\) is sampled from what distribution that has what parameter value(s)? (b) What is the probability that you will end up making money, i.e., what is \(P(W > 0)\)? (c) Let’s say instead of buying until you win, you decide you will buy exactly two tickets, then stop. What is the probability of buying a winning ticket exactly once, given that you buy at least one winning ticket?
Suppose 50% of licensed drivers in a state are insured. If three licensed drivers are selected at random, what is the expected number of insured drivers given that the number of insured drivers is odd? (Assume the state’s population is effectively infinite, so that the probability of selecting an insured driver stays constant from trial to trial.)
In an experiment, you take shots at a target until you hit that target twice. On any given shot, you have a 50% change of hitting the target. (a) What is the probability that you hit the target for the second time on your fourth shot overall? (b) You run your experiment twice. What is the probability of needing to take two shots one of the experiments to hit the target twice, and three shots during the other one to hit the target twice? Assume the results are independent (and of course identically distributed). (c) Let’s suppose you do not actually know the success probability \(p\), and you wish to determine a one-sided 90% upper bound on \(p\). As you are dealing with a discrete distribution, you need to build a
uniroot()-style interval estimator. In your code, what value would you adopt for \(q\)?You collect \(n=4\) iid samples from the following distribution: \[\begin{eqnarray*} f_X(x) = \left\{ \begin{array}{cc} 3x^2 & 0 \leq x \leq 1 \\ 0 & \mbox{otherwise} \end{array} \right. \,. \end{eqnarray*}\] (a) Write down the sampling distribution for the minimum observed value, \(X_{(1)}\). (b) The sampling distribution for the maximum observed value is \(g_{(4)}(x) = 12x^{11}\). What is \(E[X_{(4)}]\)?
You are to sample \(n = 3\) data from the following distribution: \[\begin{eqnarray*} f_X(x) = \left\{ \begin{array}{cc} x & 0 \leq x \leq \sqrt{2} \\ 0 & \mbox{otherwise} \end{array} \right. \,. \end{eqnarray*}\] (a) Specify the distribution from which \(X_{(3)}\) is to be sampled. (b) Specify the variance of the distribution you derived in part (a).
If we sample 3 iid data from a Uniform(0,1) distribution, what is the probability that the median value lies between 1/3 and 2/3?
You sample three data from a Exp(1) distribution. What is the expected value for the median datum, i.e., the second ordered datum?
Let the cdf for a given distribution be \(F_X(x) = x^3\) for \(x \in [0,1]\), and let’s assume that you have sampled \(n\) iid data from this distribution. (a) What is the pdf within the domain \(x \in [0,1]\)? (b) What is the pdf for \(X_{(n)}\) within the domain \(x \in [0,1]\)? (c) What is the cdf for \(X_{(n)}\) within the domain \(x \in [0,1]\)? (d) What is \(E[X_{(n)}]\)?
You sample \(n = 2\) iid random variables from a distribution with pdf \[\begin{eqnarray*} f_X(x) = \frac12 x \,, \end{eqnarray*}\] for \(x \in [0,2]\). (a) What is \(F_X(x)\) within the domain \([0,2]\)? (b) What is \(f_{(2)}(x)\)? (c) What is \(E[X_{(2)}]\)? (d) Are \(X_{(1)}\) and \(X_{(2)}\) independent random variables?
Find the asymptotic distribution of the MLE of \(n\) i.i.d. samples from the Bernoulli distribution with parameter \(p\). (\(p_X(x) = p^x(1-p)^{1-x}\) for \(x = \{0,1\}\) and for \(p \in (0,1)\).)
You are given \(n\) iid data that are sampled from the following pmf: \[\begin{equation*} p_X(x) = (1-p)^{x-1}p \,, \end{equation*}\] with \(0 < p < 1\) and \(x = \{1,2,3,\ldots\}\). For this distribution, \(E[X] = 1/p\) and \(V[X] = (1-p)/p^2\). (a) What is the maximum likelihood estimator for \(1/p\)? Note: you are not required to confirm that the derivative of the score function is negative at \(1/p = \widehat{1/p}_{MLE}\). Also note: a property of MLEs may help you here. (b) Write down \(V[\widehat{1/p}_{MLE}]\), i.e., the variance of the MLE for \(1/p\).
The probability mass function for the logarithmic distribution is \[\begin{eqnarray*} p_X(x) = -\frac{1}{\log(1-p)} \frac{p^x}{x} \,, \end{eqnarray*}\] where \(x \in \{1,2,3,...\}\). You sample \(n\) iid data from this distribution. Write down a sufficient statistic for \(p\).
You are given the following probability density function: \[\begin{equation*} f_X(x) = a b x^{a-1} (1-x^a)^{b-1} \,, \end{equation*}\] defined over the domain \(0 < x < 1\). \(a\) and \(b\) are the parameters of the distribution, and both are positive and real-valued. Let \(\mathbf{X} = \{X_1,\cdots,X_n\}\) be \(n\) i.i.d.~samples from this distribution. (a) If you are able to define joint sufficient statistics for \(a\) and \(b\), write them down; otherwise, explain why you cannot. (b) Now, let \(a=1\). What is a sufficient statistic for \(b\)?
You sample \(n\) iid data from the following distribution: \[\begin{eqnarray*} f_X(x) = \frac{x}{\beta^2} e^{-x/\beta} \,, \end{eqnarray*}\] where \(x \geq 0\) and \(\beta > 0\), and where \(E[X] = 2\beta\) and \(V[X] = 2\beta^2\). (a) Write down a sufficient statistic for \(\beta\) that arises directly from likelihood factorization. (b) Using your answer from part (a), determine the MVUE for \(\beta\). (c) Compute the variance of the MVUE for \(\beta\). (d) Compute the Cramer-Rao Lower Bound for the MVUE for \(\beta\).
Let \(X_1,\ldots, X_n\) be \(n\) iid samples from the following distribution, where \(\theta > 0\), \[\begin{eqnarray*} f_X(x) = \frac{1}{\theta} \exp\left(x-\frac{1}{\theta} e^x\right) \,. \end{eqnarray*}\] Note that \(e^X \sim \text{Exp}(\theta)\) (= Gamma(1,\(\theta\))) and \(Y = \sum_{i=1}^n e^{X_i} \sim \text{Gamma}(n,\theta)\) (with \(E[Y] = n\theta\) and \(V[Y] = n\theta^2\)). (a) Find a sufficient statistic for \(\theta\) using the factorization criterion. (b) Find the MVUE for \(\theta\). (c) Find the MVUE for \(\theta^2\).
Let’s assume that we have sampled \(n\) iid data, \(\{X_1,\ldots,X_n\}\), from a Maxwell-Boltzmann distribution with pdf \[\begin{eqnarray*} f_X(x) = \sqrt{\frac{2}{\pi}} \frac{x^2}{a^3} e^{-x^2/(2a^2)} \,, \end{eqnarray*}\] where \(x > 0\) and \(a > 0\). The expected value and variance for an MB-distributed random variable are \[\begin{eqnarray*} E[X] = 2 a \sqrt{\frac{2}{\pi}} ~~~ \mbox{and} ~~~ V[X] = a^2 \frac{(3 \pi - 8)}{\pi} \end{eqnarray*}\] respectively. (a) Identify a sufficient statistic for \(a^2\). (b) Derive \(E[X^2]\). (Hint: there is no need for integration here.) (c) Determine the MVUE for \(a^2\). (d) Can we use an invariance principle to state that the MVUE for \(a\) is \((\widehat{a^2}_{MVUE})^{1/2}\)?
You sample a single datum \(X\) from the following pdf: \[\begin{eqnarray*} f_X(x) = \frac{\theta}{2^\theta} x^{\theta-1} \,, \end{eqnarray*}\] where \(x \in [0,2]\) and \(\theta > 0\). Construct the most powerful level-\(\alpha\) test of \(H_o: \theta = \theta_o\) versus \(H_a: \theta = \theta_a\), where \(\theta_a > \theta_o\). Is your hypothesis test a uniformly most powerful hypothesis test?
A common distribution used for the lengths of life of physical systems is the Weibull. Let \(\{X_1,\ldots,X_n\}\) be \(n\) iid data sampled from this distribution: \[\begin{eqnarray*} f_X(x) = \frac{\theta}{\beta} \hspace{1mm} x^{\theta-1} \hspace{1mm} \exp\left(-\frac{x^\theta}{\beta}\right) \hspace{5mm} x,\beta, \theta >0 \end{eqnarray*}\] Assume that \(\theta\) is known and that \(\beta\) is freely varying, and that we are interested in finding the most powerful test of \(H_o: \beta = \beta_o\) versus \(H_a: \beta = \beta_a\), where \(\beta_a > \beta_o\), at the level \(\alpha\).
- What is a sufficient statistic for \(\beta\)? (Do not include a minus sign.)
- Working with the Weibull directly is difficult; however, it turns out that \(X^\theta \sim \text{Exp}(\beta)\). What is the distribution of the sufficient statistic found in part (a), and what are the parameter values? (This will require examining the gamma distribution and its properties.)
- Write, in
Rcode, the rejection-region boundary for the test.
- Let \(\{X_1,\ldots,X_n\}\) be \(n\) iid data sampled from the following distribution: \[\begin{eqnarray*} f_{X}(x) = \left\{ \begin {array}{ll} \frac{1}{\theta}\exp\left(-\frac{1}{\theta}(x-b)\right) & x > b, \theta > 0 \\ 0&\mbox{otherwise} \end{array} \right. \,. \end{eqnarray*}\]
- Derive the moment-generating function for \(X\).
- Now derive the mgf for \(\sum_{i=1}^n X_i\).
- The answer for (b) contains the term \(e^{nbt}\). Going back to our original discussion of the method of moment-generating functions, this means that we can write that \(\sum_{i=1}^n X_i = nb + \sum_{i=1}^n U_i\). What distribution is \(\sum_{i=1}^n U_i\) sampled from? (Hint: look at the the rest of the mgf for \(\sum_{i=1}^n X_i\) and, if necessary, refer back to the previous problem.)
- Write, in
Rcode, the rejection-region boundary for the \(\alpha\)-level test of \(H_o : \theta = \theta_o\) versus \(H_a : \theta < \theta_o\). Is this a uniformly most powerful test of these hypotheses?
In an experiment, you sample \(n\) data from the distribution: \[\begin{eqnarray*} f_X(x) = \theta e^{-\theta x} \,, \end{eqnarray*}\] where \(x \geq 0\), \(\theta > 0\), and \(E[X] = 1/\theta\). You wish to test the null hypothesis \(H_o : \theta_o = 4\) versus \(H_a : \theta_a = 2\). (a) Define the most powerful hypothesis test. By “define,” we mean write down a rejection region of the form \(Y < y_{\rm RR}\) or \(Y > y_{\rm RR}\), where you plug in a specific statistic for \(Y\). (You cannot evaluate \(y_{\rm RR}\) given the information you have here…that can stay as is.) (b) The cdf of the sampling distribution for the appropriate statistic in part (a) is \(\gamma(n,\theta y)/(n-1)!\), where \(\gamma(\cdot,\cdot)\) is the lower incomplete gamma function. Given this information, and given what you would have to do to define the rejection region boundary, can you conclude that we are defining a uniformly most powerful test?
Let’s assume that we have sampled \(n\) iid data from a Binom(\(k,p\)) distribution, and that we wish to test \(H_o: p = p_o\) versus \(H_a: p > p_o\). For our statistic, we will use \(Y = \sum_{i=1}^n X_i\). (a) What is the sampling distribution for \(Y\)? Provide the name and the value(s) of the parameters. (b) You code elements of the test in
R. Assume you have the initialized variablesalpha,n,k,y.obs,p.o, andp.aat your disposal. Write out the (one-line!) function call you’d use to compute the rejection region boundary. (c) Now provide code of the \(p\)-value. Include a discreteness correction factor if it is needed.The negative inverse link function is \(-(Y \vert x)^{-1}\). Assume that we are in a simple setting (i.e., that there is one predictor variable), and write the regression line formula \(Y \vert x\) as a function of \(\beta_0\), \(\beta_1\), and \(x\).
You use
Rto learn a logistic regression model, and you observe the output shown below: (a) What is the sample size \(n\)? (Hint: take into account how many parameter values are being estimated to convert a number shown in the output to the sample size.) (b) What is the value of \(-2\log\mathcal{L}_{\rm max}\) for the model in which \(\beta_1\) is set to zero? (c) What is the value of \(O(x)\) for \(x = 0\)? You may leave your answer in the form \(e^a\) or \(\log(a)\) or \(\sqrt{a}\), etc., while being sure to fill in the value of the constant \(a\). (d) Do the odds increase as \(x\) increases, or do the odds decrease as \(x\) increases?
Below is the observed output from
R’sglm()function when learning a logistic regression model. For these data, Class 0 isNo(not a student) and Class 1 isYes(is a student). (a) If the balance is $589, then the predicted probability that the datum belongs to theYesclass is 0.1. What is the odds ratio for $589 dollars? (b) What is the odds ratio if the balance is $689? (c) For the first datum, the observed response isNoand the predicted probability that the datum is of theYesclass is 0.07. Compute the deviance for this datum. (d) Whoops…the null deviance value got expunged from the output. Would this value be higher or lower than the observed residual deviance value?
Deviance Residuals:
Min 1Q Median 3Q Max
-1.1243 -0.5539 -0.4409 -0.3460 2.4901
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -3.0616324 0.3936314 -7.778 7.37e-15 ***
Balance 0.0014684 0.0004124 3.561 0.00037 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual deviance: 221.47 on 308 degrees of freedom
AIC: 225.47 Refer to the displayed data below. Here,
x1andx2are the two predictor variables, and \(Y\) is the response variable. Use these data to learn a Naive Bayes model and use that model to compute \(p(0 \vert \mbox{Yes},\mbox{False}) = p(0 \vert \mbox{Y},\mbox{F})\). Leave your answer as a fraction. Assume that \(p(C_k) = n_k/n\), and that you would estimate \(p(x \vert C_k)\) as the proportion of times you observe a particular datum value \(x\) (e.g., True) given \(C_k\).
You are given the following pdf: \[\begin{eqnarray*} f_X(x) = \left\{ \begin{array}{cc} 2(1-x) & 0 \leq x \leq 1 \\ 0 & \mbox{otherwise} \end{array} \right. \,. \end{eqnarray*}\] An associated cost is \(C = 10X\). (a) Identify the “named” distribution for \(X\) and state its parameters. (b) Given your answer for (a), determine \(E[X]\) and \(E[X^2]\). (c) Now determine \(E[C]\) and \(V[C]\).
You are given the following cdf: \[\begin{eqnarray*} F_X(x) = \left\{ \begin{array}{cc} 0 & x < 0 \\ 6x^2 - 8x^3 + 3x^4 & 0 \leq x \leq 1 \\ 1 & x > 1 \end{array} \right. \,. \end{eqnarray*}\] (a) \(F_X(x)\) is the cdf for what “named” distribution? (b) What is the expected value of \(X\)?
You are given \(X \sim\) Beta(2,3). What is \(E[X^2]\)?
You sample 3 data from a Beta(3,1) distribution. (a) Write down the pdf for the median of the sampled data. (b) Compute the expected value for the median of the sampled data.
You are given the following distribution: \[\begin{eqnarray*} f_X(x) = c x (1-x) \,, \end{eqnarray*}\] where \(x \in [0,1]\) and \(c\) is a constant. (a) Identify this distribution by name and provide the value(s) of its parameter(s). (b) Determine the numerical value of the constant \(c\). (c) Is the distribution symmetric about its mean value or it is a skewed distribution? (d) Compute \(P(X \leq 1/4 \vert X \leq 1/2)\). Leave your answer as a fraction.
Twenty-one (21) students enter a hallway off of which are three rooms. A researcher expects each student to randomly choose a room to enter (and to stay in!). That researcher observes that 10 students choose Room A, 5 students choose Room B, and 6 students choose Room C, and she decides to use these data to perform a test of the null hypothesis \(p_1 = p_2 = p_3\) at the level \(\alpha = 0.1\). (a) Choose an appropriate hypothesis test and evaluate the test statistic. To be clear, your final answer should be a number. (b) What is the number of degrees of freedom associated with the test statistic? (c) The rejection region boundary value is 4.61. Do we reject the null hypothesis?
A political scientist has developed four pamphlets with different types of information about climate change – one focused on environmental impact, one on economic impact, one on socio-cultural impact, and one about the origins of climate change. She prints 100 of each and randomly gives them out, asks people to read them, and records their answer to the question: how much money should the government spend on counteracting climate change? The answer options are: [a] more than, [b] as much as, and [c] less than they currently do. She plans to do a chi-square test to check whether willingness to spend government funding is related to which pamphlet the respondent read. (Note that she does not segment the respondents into groups.) (a) What kind of chi-square test is conducted here (goodness-of-fit, independence, or homogeneity)? (b) The observed test statistic turns out to be \(w_{\rm obs} = 24.3\). How many terms did the researcher have to sum over to compute this statistic? (c) The test statistic follows a chi-square distribution with \(m\) degrees of freedom. What is the value of \(m\)? (d) Which of the following expressions corresponds to the \(p\)-value associated with the test carried out in part (a): (i) \(P(W \geq w_{\rm obs})\), (ii) \(P(W \leq w_{\rm obs})\), (iii) \(P(\frac{(n-1) W }{ \sigma^2} \geq w_{\rm obs})\), or (iv) \(P(\frac{(n-1) W}{\sigma^2} \leq w_{\rm obs})\)? (\(W\) is the random variable, chi-square-distributed for \(m\) degrees of freedom; \(n\) is the sample size; and \(\sigma^2\) is the population variance.)
You are recording the amount of time that elapses between when one person walks through a particular door until the next person walks through that same door. You have a weird stopwatch that changes from 0 to 1 after one minute, and from 1 to 2 after two minutes. That’s it. You take 100 measurements, and your data are given below. You wish to test the null hypothesis that each elapsed time is sampled from an exponential distribution with mean \(\beta\) = 1 minute. (a) Under this null hypothesis, the probability that someone ends up in the category “1-2 minutes” is \(\int_1^2 e^{-x} dx\). Explain why this is and calculate the probability. (b) Carry out an appropriate test to test the null hypothesis, provide either the rejection region or the \(p\)-value, and state your conclusion. Assume \(\alpha = 0.05\). (c) A friend of yours decides they will repeat the experiment you’ve done, including the statistical analysis, but he is in a hurry and decides that he will only take 10 measurements overall. Explain to your friend why his experimental “design” is flawed.
| 0-1 min | 1-2 min | >2 min |
|---|---|---|
| 52 | 23 | 25 |
You play a (long) game in which you shoot 180 shots at a 3-by-3 square target, inside of which is a 1-by-1 square bullseye. Of your shots, 30 hit the bullseye while the remainder all hit the target, but hit outside the bullseye. You wish to test the null hypothesis that your shots hit the target at random locations. (a) Specify the number of shots that are expected to hit outside of, and inside of, the bullseye if the null hypothesis is correct. (b) Compute the value of an appropriate statistic for this test. (c) Specify the sampling distribution for this statistic (if the null hypothesis is correct); give the name and the values of any distribution parameters. (d) The rejection region boundary for this test is 3.841. State a conclusion regarding the null hypothesis: “reject” or “fail to reject.”
We collect \(k\) independent datasets, and perform hypothesis tests for the population mean given each. When we are done, we have \(k\) separate \(p\)-values, which are all independent of each other. In every case, it turns out that the the null hypothesis is correct. Let \(X\) represent the number of \(p\)-values that you observe are less than \(\alpha\), the Type I error. Write down a general expression for the probability \(P(X = x)\).
We are given three iid data sampled according to a geometric distribution with parameter \(p\). What is the distribution of \(Y = X_1 + X_2 + X_3\)? State both the name of the distribution, and specific values for its parameters.
We sample a random variable \(X_1\) from a degenerate distribution: \[\begin{align*} p_X(x) = 1 \,, \end{align*}\] for \(x = a\). We then sample another random variable, \(X_2\), from a Bernoulli distribution. Assume \(X_1\) and \(X_2\) are independent. Derive the moment-generating functions for \(X_1\) and \(X_2\) and use them to compute the expected value and the variance of the sum \(X_1 + X_2\).
We play a game in which we sample data from a standard normal distribution at a rate of one datum per second. (a) Write down the probability of observing exactly one datum with a value \(>\) 3 during a 100-second game. Leave the answer in terms of a CDF symbol or an inverse CDF symbol, whichever is appropriate. (b) In another version of the game, we play until we observe one datum with value \(>\) 3. How long, in (integer) seconds, would the average game last? Again, leave your answer in terms of either a CDF or an inverse CDF symbol.
Let \(X_1\) and \(X_2\) be iid random variables drawn from the distribution \(f_X(x) = e^{-x}\) for \(x \geq 0\). (a) Write down the pdf for the smaller of the two values \(X_1\) and \(X_2\). (b) Compute the moment-generating function for the smaller of the two values \(X_1\) and \(X_2\). (c) Using the results from (a) and (b), identify the distribution of the smaller of the two values \(X_1\) and \(X_2\) (by name and parameter value).
The probability density function for the beta prime distribution is \[\begin{align*} f_X(x) = \frac{x^{\alpha-1}(1+x)^{-\alpha-\beta}}{B(\alpha,\beta)} ~~~~~~ x \in [0,1] ~~~~~~ \alpha,\beta > 0 \,. \end{align*}\] What is the expected value of \(X\)? (Note that this expression will only be valid for values \(\beta > 1\).) Hint: consider working with the expected value of \(1+X\) instead of \(X\) itself.
We conduct an experiment involving 24 trials, after which we record the number of counts seen in each of three separate bins; the data we observe are 8, 8, and 8. Before the experiment began, we had an expectation that one-quarter of the overall number of counts would be recorded in the first bin, that one-quarter of the counts would be recorded in the second bin, and that one-half would be recorded in the third bin. We now test this hypothesis at the level \(\alpha = 0.05\). (a) What is the test statistic? (b) Write down an
Rfunction call that outputs the rejection-region boundary for this test. (c) Write down anRfunction call that outputs the \(p\)-value for this test. (d) The observed data are sampled according to what discrete family of distributions?