4 The Poisson (and Related) Distributions

4.1 Motivation

One of the challenges of a Prussian soldier’s life in the 19th century was avoiding being kicked by horses. This was no trivial matter: over one 20-year period, 122 soldiers died from horse-kick-related injuries. The data below are from the 1925 R. A. Fisher work Statistical Methods for Research Workers; they are a subset of the original data that were compiled earlier by the statistician Ladislaus Bortkiewicz.

\(x\)	\(N(x)\)
0	109
1	65
2	22
3	3
4	1

\(x\) is the number of deaths observed in any one Prussian army corp in any one year, and \(N(x)\) is the number of corps-years in which \(x\) deaths were observed. (\(N(x)\) sums to \(20 \cdot 10 = 200\), reflecting that the compiled data represent 10 army corps observed over a 20-year period.)

The data presented above are an example of a process, i.e., a sequence of observations, but we can immediately see that unlike the case with coin flips, this process is not a Bernoulli process. That’s because the number of possible outcomes is greater than two (0 and 1); in fact, the number of possible outcomes is countably infinite, so we could not even call this a multinomial process. Well, the reader might say, we could simply discretize the data more finely, so that the number of possible outcomes is at least finite (multinomial) or better yet falls to two (Bernoulli). Let’s get monthly data, or daily data, or hourly data. However, there is no time period \(\Delta t\) for which the number of possible outcomes is limited to some maximum value: in theory, an infinite number of soldiers could die in the same second, or even the same nanosecond, etc.

But let’s keep playing with this idea of making the time periods smaller and smaller. Let the number of time periods into which we divide our observation interval, \(k\), go to infinity such that the probability of observing a horse-kick death \(p \rightarrow 0\) and such that \(kp \rightarrow \lambda\), where \(\lambda\) is a constant. Under these conditions, as we will see in the next section, the binomial distribution transforms into the Poisson distribution, which Bortkiewicz dubbed the law of small numbers. Before we go to the section, though, let’s define the Poisson distribution in words: it gives the probability of observing a particular number of events (“counts”) in a fixed interval of space and/or time, assuming there is a constant mean rate of events and the occurrence of any one event is independent of the occurrence of other events.

(For those who do not wish to wait until the section on point estimation to know the final answer: \(\hat{\lambda}_{MLE} = 0.61\), i.e., if the data are plausibly Poisson distributed [which is another question to ask entirely!], the true rate of death is estimated to be 0.61 soldiers per corps per year.)

4.2 Probability Mass Function

Recall: a probability mass function is one way to represent a discrete probability distribution, and it has the properties (a) \(0 \leq p_X(x) \leq 1\) and (b) \(\sum_x p_X(x) = 1\), where the sum is over all values of \(x\) in the distribution’s domain.

To derive the Poisson probability mass function, we start by writing down the binomial distribution, setting \(p\) to \(\lambda/k\), where \(\lambda\) is an arbitrarily valued positive constant, and letting \(k\) go to infinity: \[\begin{align*} P(X=x) &= \binom{k}{x} p^x (1-p)^{k-x} \\ &= \frac{k!}{x!(k-x)!} \left(\frac{\lambda}{k}\right)^x \left(1-\frac{\lambda}{k}\right)^{k-x} \\ &= \frac{k!}{(k-x)! k^x} \frac{\lambda^x}{x!} \left(1-\frac{\lambda}{k}\right)^{k-x} \\ &= \left(\frac{k}{k}\right) \left(\frac{k-1}{k}\right) \cdots \left(\frac{k-x+1}{k}\right) \left(\frac{\lambda^x}{x!}\right) \left(1-\frac{\lambda}{k}\right)^{k-x} \rightarrow \frac{\lambda^x}{x!} \left(1-\frac{\lambda}{k}\right)^{k-x} ~\mbox{as}~~ k \rightarrow \infty \\ &= \frac{\lambda^x}{x!} \left(1-\frac{\lambda}{k}\right)^k \left(1-\frac{\lambda}{k}\right)^{-x} \rightarrow \frac{\lambda^x}{x!} \left(1-\frac{\lambda}{k}\right)^k ~\mbox{as}~~ k \rightarrow \infty \,. \end{align*}\] At this point, we concentrate on the parenthetical term above. Given that \[ \lim_{k \rightarrow \infty} \left(1 - \frac{1}{k}\right)^k = e^{-1} \,, \] we can state that \[ \lim_{k \rightarrow \infty} \left(1 - \frac{1}{k/\lambda}\right)^{k/\lambda} = e^{-1} \implies \lim_{k \rightarrow \infty} \left(1 - \frac{1}{k/\lambda}\right)^k = e^{-k} \,. \] We are now in a position to write down the probability mass function for a Poisson random variable (see Figure 4.1): \[ P(X=x) = p_X(x) = \frac{\lambda^x}{x!} e^{-\lambda} ~\mbox{where}~ \lambda > 0 ~\mbox{and}~ x \in [0,\infty) \,. \] A Poisson random variable converges in distribution to a normal random variable as \(\lambda \rightarrow \infty\), a result which affects how Poisson-distributed data have historically been treated in, e.g., hypothesis test settings. (We will elaborate on this point when we return to the chi-square goodness of fit test later in the chapter.) To indicate that we have sampled a datum from a Poisson distribution, we write \(X \sim\) Poisson(\(\lambda\)). The expected value and variance of the Poisson distribution are \(E[X] = \lambda\) and \(V[X] = \lambda\), respectively; the former is derived below in an example.

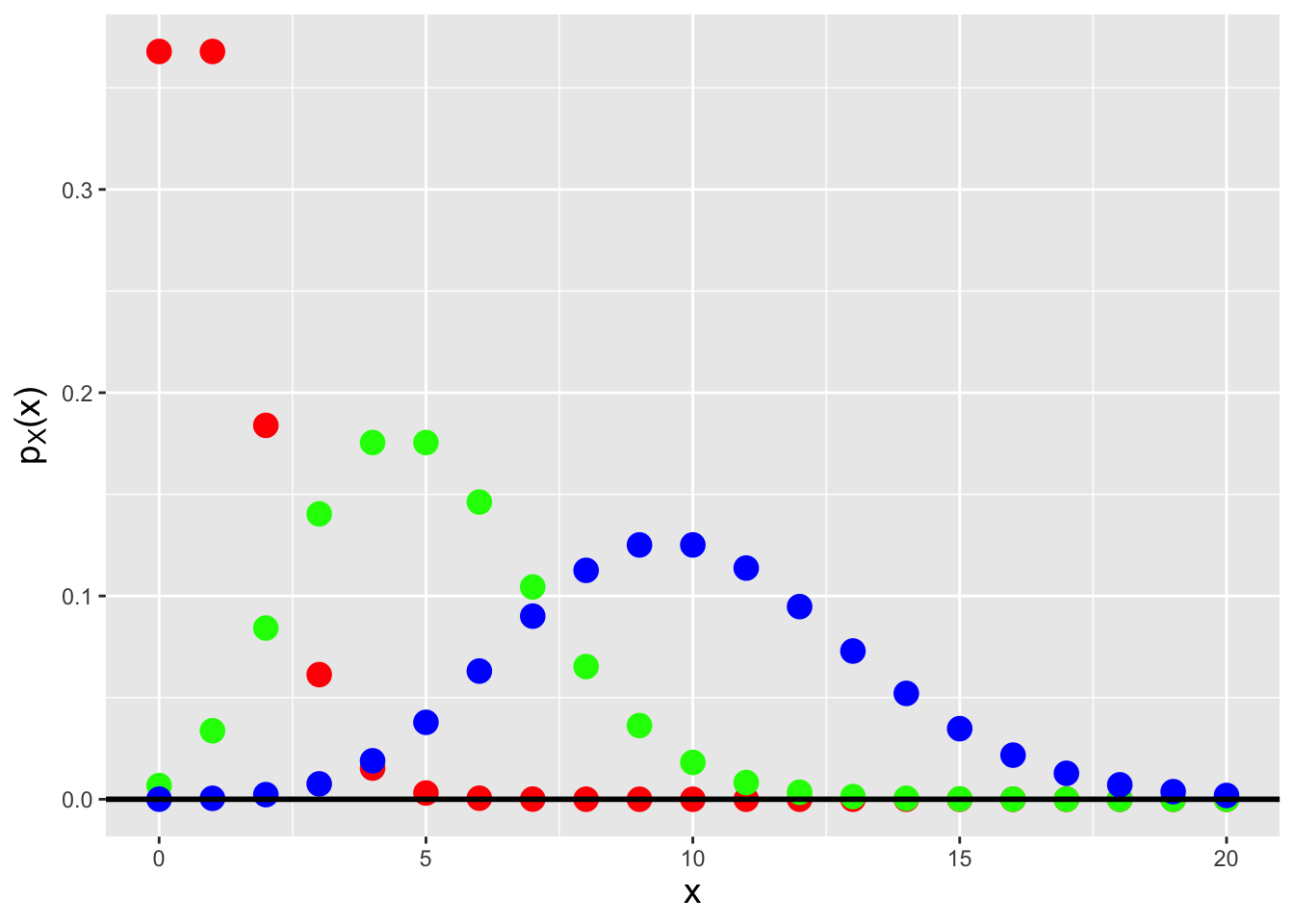
Figure 4.1: Poisson probability mass functions for \(\lambda = 1\) (red), 5 (green), and 10 (blue).

---

4.2.1 The Expected Value of a Poisson Random Variable

Recall: the expected value of a discretely distributed random variable is \[ E[X] = \sum_x x p_X(x) \,, \] where the sum is over all values of \(x\) within the domain of the pmf p_X(x). The expected value is equivalent to a weighted average, with the weight for each possible value of \(x\) given by \(p_X(x)\).

For a Poisson distribution, the expected value is \[ E[X] = \sum_{x=0}^\infty x \frac{\lambda^x}{x!} e^{-\lambda} = \sum_{x=1}^\infty x \frac{\lambda^x}{x!} e^{-\lambda} = \sum_{x=1}^\infty \frac{\lambda^x}{(x-1)!} e^{-\lambda} \,. \] The goal is to move constants into or out of the summation so that the summation becomes one of a probability mass function over its entire domain. Here, we move \(\lambda\) out of the summation, and make the substitution \(y = x-1\); the summand then takes on the form of a Poisson pmf, summed over its entire domain: \[ E[X] = \lambda \sum_{x=1}^\infty \frac{\lambda^{x-1}}{(x-1)!} e^{-\lambda} = \lambda \sum_{y=0}^\infty \frac{\lambda^{y}}{y!} e^{-\lambda} = \lambda \,. \] Note that a similar calculation that starts with the derivation of \(E[X(X-1)]\) yields the Poisson variance.

4.3 Cumulative Distribution Function

Recall: the cumulative distribution function, or cdf, is another means by which to encapsulate information about a probability distribution. For a discrete distribution, it is defined as \(F_X(x) = \sum_{y\leq x} p_Y(y)\), and it is defined for all values \(x \in (-\infty,\infty)\), with \(F_X(-\infty) = 0\) and \(F_X(\infty) = 1\).

For the Poisson distribution, the cdf is \[ F_X(x) = \sum_{y=0}^{\lfloor x \rfloor} p_Y(y) = \sum_{y=0}^{\lfloor x \rfloor} \frac{\lambda^y}{y!} \exp(-\lambda) = \frac{\Gamma(\lfloor x+1 \rfloor,\lambda)}{\lfloor x \rfloor !} \,, \] where \(\lfloor x \rfloor\) denotes the floor function, which returns the largest integer that is less than or equal to \(x\) (e.g., if \(x\) = 8.33, \(\lfloor x \rfloor\) = 8), and where \(\Gamma(\cdot,\cdot)\) is the upper incomplete gamma function \[ \Gamma(\lfloor x+1 \rfloor,\lambda) = \int_{\lambda}^\infty u^{\lfloor x \rfloor} e^{-u} du \,. \] (An example of an R function which computes the upper incomplete gamma function is incgam() in the pracma package.) As we are dealing with a probability mass function, the cdf is a step function, as illustrated in the left panel of Figure 4.2. Recall that because of the step-function nature of the cdf, the form of inequalities in a probabilistic statement matter: e.g., \(P(X < x)\) and \(P(X \leq x)\) will not be the same if \(x\) is zero or a positive integer.

Recall: an inverse cdf function \(x = F_X^{-1}(q)\) takes as input a distribution quantile \(q \in [0,1]\) and returns the value of \(x\). A discrete distribution has no unique inverse cdf; it is convention to utilize the generalized inverse cdf, \(x = \mbox{inf}\{x : F_X(x) \geq q\}\), where “inf” indicates that the function is to return the smallest value of \(x\) such that \(F_X(x) \geq q\).

In the right panel of Figure 4.2, we display the inverse cdf for the same distribution used to generate the figure in the left panel (\(\lambda = 2\)). Like the cdf, the inverse cdf for a discrete distribution is a step function.

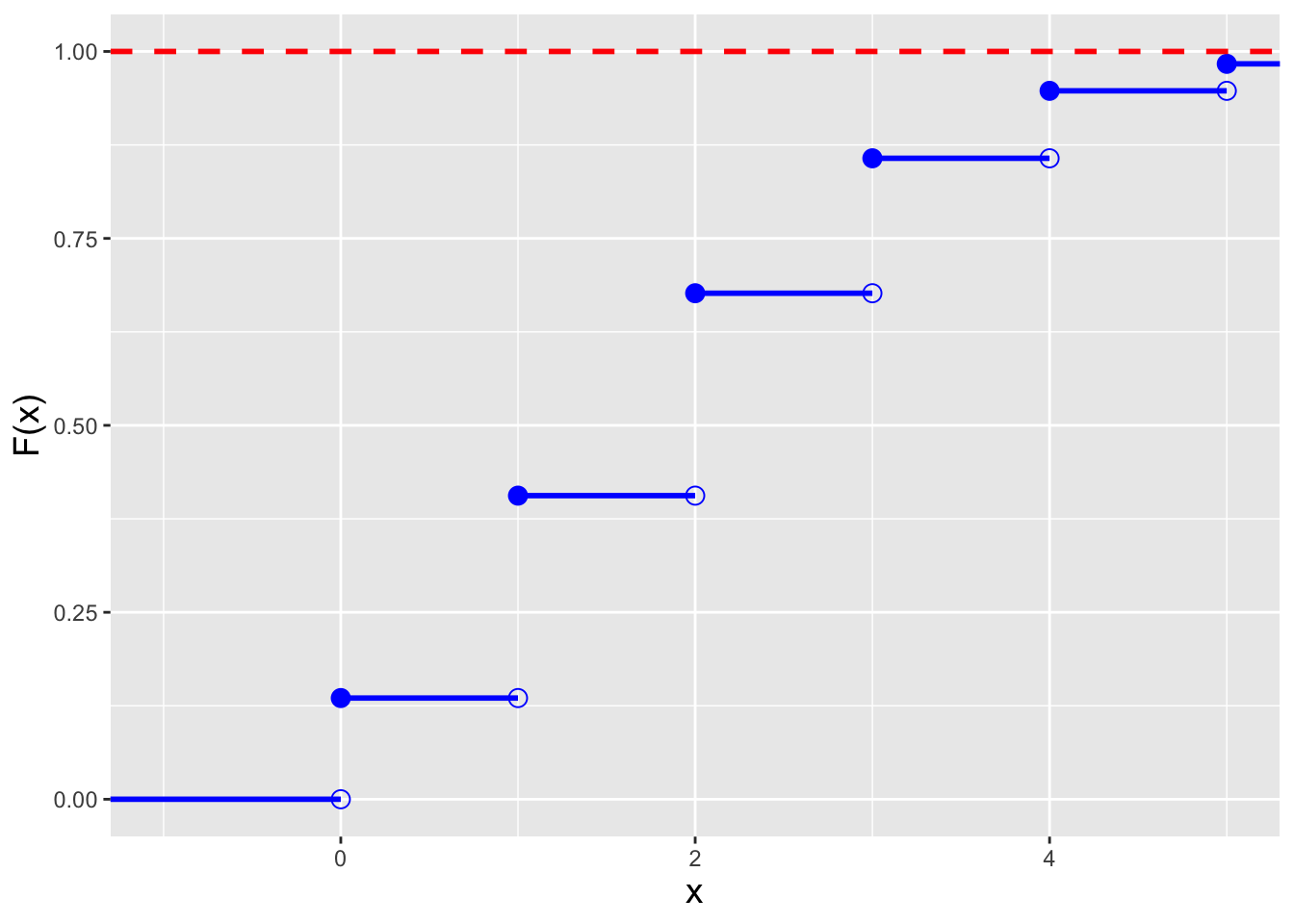
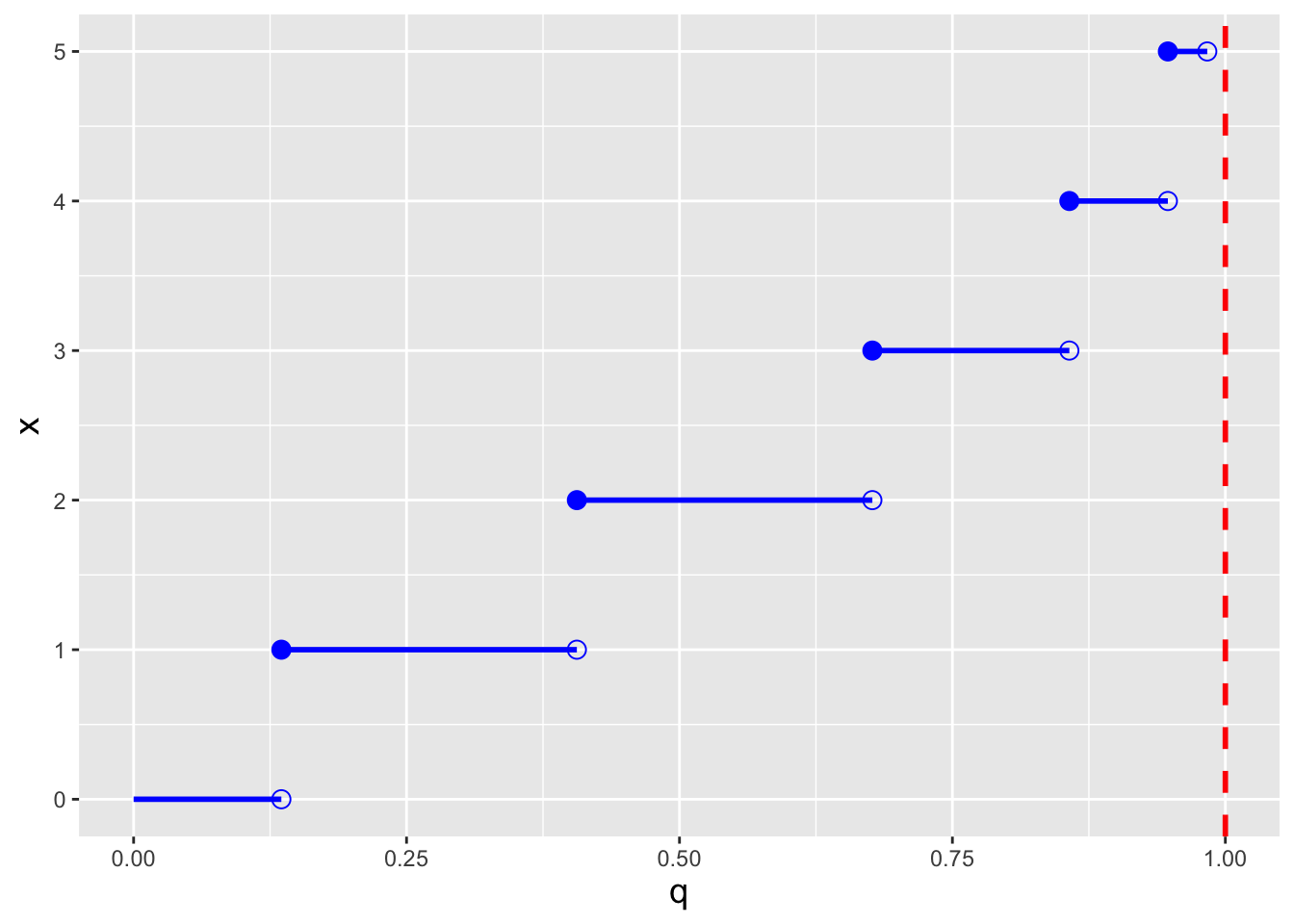
Figure 4.2: Illustration of the cumulative distribution function \(F_X(x)\) (left) and inverse cumulative distribution function \(F_X^{-1}(q)\) (right) for a Poisson distribution with \(\lambda=2\). Note that because the domain of the Poisson distribution is countably infinite, we do observe any values of \(x\) for which \(F_X(x) = 1\).

---

4.3.1 Computing Probabilities

1. If \(X \sim\) Poisson(5), which is \(P(4 \leq X < 6)\)?

We first note that due to the form of the inequality, we do not include \(X=6\) in the computation. Thus \(P(4 \leq X < 6) = p_X(4) + p_X(5)\), which equals \[ \frac{5^4}{4!}e^{-5} + \frac{5^5}{5!}e^{-5} = \frac{5^4}{4!}e^{-5} \left( 1 + \frac{5}{5} \right) = 2\frac{5^4}{4!}e^{-5} = 0.351\,. \] If we utilize R:

dpois(4,lambda=5) + dpois(5,lambda=5)

## [1] 0.3509347

Note that we can take advantage of R’s vectorization capabilities by writing

sum(dpois(4:5,lambda=5))

## [1] 0.3509347

This approach is far more convenient than writing out a string of calls to dpois(), particularly when the number of values of \(x\) to sum over becomes large. We can also utilize cdf functions here: \(P(4 \leq X < 6) = P(X < 6) - P(X < 4) = P(X \leq 5) - P(X \leq 3) = F_X(5) - F_X(3)\), which in R is computed as follows:

ppois(5,lambda=5) - ppois(3,lambda=5)

## [1] 0.3509347

2. If \(X \sim\) Poisson(5), what is the value of \(a\) such that \(P(X \leq a) = 0.9\)?

First, we set up the inverse cdf formula: \[ P(X \leq a) = F_X(a) = 0.9 ~~ \Rightarrow ~~ a = F_X^{-1}(0.9) \] Note that we didn’t do anything differently here than we would have done in a continuous distribution setting…and we can proceed directly to R because it utilizes the generalized inverse cdf algorithm.

qpois(0.9,lambda=5)

## [1] 8

4.4 Linear Functions of Random Variables

Let’s assume we are given \(n\) iid Poisson random variables: \(X_1,X_2,\ldots,X_n \sim\) Poisson(\(\lambda\)). What is the distribution of the sum \(Y = \sum_{i=1}^n X_i\)?

Recall: the moment-generating function, or mgf, is a means by which to encapsulate information about a probability distribution. When it exists, the mgf is given by \(m_X(t) = E[e^{tX}]\). Also, if \(Y = \sum_{i=1}^n a_iX_i\), then \(m_Y(t) = m_{X_1}(a_1t) m_{X_2}(a_2t) \cdots m_{X_n}(a_nt)\); if we can identify \(m_Y(t)\) as the mgf for a known family of distributions, then we can immediately identify the distribution for \(Y\) and the parameters of that distribution.

The mgf for a Poisson random variable \(X\) is \[ m_X(t) = \exp\left[\lambda\left(e^t-1\right)\right] \,. \] (We derive this in an example below.) Thus the mgf for \(Y = \sum_{i=1}^n X_i\) is \[ m_Y(t) = \exp\left[\lambda\left(e^t-1\right)\right] \cdots \exp\left[\lambda\left(e^t-1\right)\right] = \exp\left[(\lambda+\cdots+\lambda)(e^t-1)\right] = \exp\left[n\lambda(e^t-1)\right] \,. \] This mgf retains the form of a Poisson mgf. We thus see that the sum of Poisson-distributed random variables is itself Poisson distributed with parameter \(n\lambda\), i.e., \(Y = \sum_{i=1}^n X_i \sim\) Poisson(\(n\lambda\)).

While we can identify the distribution of the sum by name, we cannot say the same about the sample mean. If \(\bar{X} = \left(\sum_{i=1}^n X_i\right)/n\), then \[ m_{\bar{X}}(t) = \exp\left[n\lambda(e^{t/n}-1)\right] \,. \] We cannot identify a named family of distributions with this specific mgf. However, we do know the distribution: it has a pmf that is identical in form to that of the Poisson distribution, but has the domain \(\{0,1/n,2/n,...\}\). (We can derive this result mathematically by making the transformation \(\sum_{i=1}^n X_i \rightarrow (\sum_{i=1}^n X_i)/n\).) We could define the pmf ourselves using our own R function, but there is no real need to: if we wish to construct a confidence interval for \(\lambda\), we can simply construct one for \(n\lambda\) using the sum of the data as a statistic, and then divide the bounds by \(n\). (We could also, in theory, utilize the Central Limit Theorem if \(n \gtrsim 30\), but there is absolutely no reason to do that to make inferences about \(\lambda\): we know the distribution of the sum of the data exactly, and thus there is no need to fall back upon approximations.)

---

4.4.1 The Moment-Generating Function of a Poisson Random Variable

The moment-generating function for a random variable \(X\) is found by utilizing the Law of the Unconscious Statistician and computing \(E[e^{tX}]\). If \(X\) is a Poisson random variable, then \[\begin{align*} m_X(t) = E[e^{tX}] &= \sum_{x=0}^\infty e^{tx} p_X(x) = \sum_{x=0}^\infty e^{tx} \frac{\lambda^x}{x!} e^{-\lambda} = e^{-\lambda} \sum_{x=0}^\infty \frac{\lambda^x}{x!} e^{tx} \\ &= e^{-\lambda} \left[ 1 + \lambda e^t + \frac{\lambda^2}{2!}e^{2t} + \ldots \right] = e^{-\lambda} \left[ 1 + y + \frac{y^2}{2!} + \ldots \right] \\ &= e^{-\lambda} e^y = \exp(-\lambda) \exp(\lambda e^t) = \exp[\lambda(e^t-1)] \,. \end{align*}\]

---

4.4.2 The Distribution of the Difference of Two Poisson Random Variables

Let’s assume that we are pointing a camera at an object, such as a star. A star gives off photons at a particular average rate \(\alpha_S\) (with units of, e.g., photons per second). Thus if we open the shutter for a length of time \(t\), the number of photons we observe from the star is a Poisson random variable \(S \sim\) Poisson(\(\lambda_S=\alpha_St\)). But the star is not the only object in the field of view; there may be other objects in the background that give off photons at a rate \(\alpha_B\), and the number of photons we observe from the background will be \(B \sim\) Poisson(\(\lambda_B=\alpha_Bt\)). Thus what we record is not \(S\), but \(T = S+B\)…so how can we make statistical inferences about \(S\) itself?

One possibility is to point the camera to an “empty” field near the star, and record some number of photons \(B\) over the same amount of time. Then we can estimate \(S\) using \(S = T - B\). What is the distribution of \(S\)?

We can utilize the method of moment-generating functions and write that \[\begin{align*} m_S(t) = m_T(t) m_B(-t) &= \exp[\lambda_T(e^t-1)] \exp[\lambda_B(e^{-t}-1)] \\ &= \exp[\lambda_T(e^t-1) + \lambda_B(e^{-t}-1)] \\ &= \exp[-(\lambda_T+\lambda_B) + \lambda_Te^t + \lambda_Be^{-t}] \,, \end{align*}\] where \(\lambda_T = \lambda_S+\lambda_B = (\alpha_S+\alpha_B)t\). At first, utilizing the method of mgfs appears to be a fool’s errand: this is not an mgf we know. But it turns out that the family of distributions associated with this mgf does have a name: \(S = T-B\) is a Skellam-distributed random variable, with mean \(\lambda_T-\lambda_B\) and variance \(\lambda_T+\lambda_B\). We can work with this distribution to, e.g., construct confidence intervals for \(\mu_S\), etc., if we so choose.

4.5 Point Estimation

In previous chapters, we describe two commonly used point estimators: the maximum likelihood estimator and the minimum variance unbiased estimator. We review both below, in the context of estimating the Poisson \(\lambda\) parameter, and then for completeness introduce one last, less-commonly used approach, the so-called method of moments.

Recall: the bias of an estimator is the difference between the average value of the estimates it generates and the true parameter value. If \(E[\hat{\theta}-\theta] = 0\), then the estimator \(\hat{\theta}\) is said to be unbiased.

Recall: the value of \(\theta\) that maximizes the likelihood function is the maximum likelihood estimate, or MLE, for \(\theta\). The maximum is found by taking the (partial) derivative of the (log-)likelihood function with respect to \(\theta\), setting the result to zero, and solving for \(\theta\). That solution is the maximum likelihood estimate \(\hat{\theta}_{MLE}\). Also recall the invariance property of the MLE: if \(\hat{\theta}_{MLE}\) is the MLE for \(\theta\), then \(g(\hat{\theta}_{MLE})\) is the MLE for \(g(\theta)\).

First, let’s take the logarithm of the likelihood function written out above: \[ \ell(\lambda \vert \mathbf{x}) = \left(\sum_{i=1}^n x_i\right) \log \lambda - n \lambda - \log\left(\prod_{i=1}^n x_i!\right) \,. \] (Note that we technically need not write down any terms that do not include \(\lambda\), like the last term, as such terms will disappear entirely during differentiation.) The derivative of \(\ell(\lambda \vert \mathbf{x})\) with respect to \(\lambda\) is \[ \frac{d\ell}{d\lambda} = \left(\frac{1}{\lambda}\sum_{i=1}^n x_i \right) - n \,. \] Setting the derivative to zero and rearranging terms, we find that \[ \hat{\lambda}_{MLE} = \frac{1}{n} \sum_{i=1}^n X_i = \bar{X} \] is the MLE for \(\lambda\). By the general rule introduced in Chapter 1, \(E[\hat{\lambda}_{MLE}] = E[\bar{X}] = \lambda\) (so \(\hat{\lambda}_{MLE}\) is an unbiased estimator), and \(V[\hat{\lambda}_{MLE}] = \lambda/n\) (so \(\hat{\lambda}_{MLE}\) is a consistent estimator, since \(\hat{\lambda}_{MLE} \rightarrow \lambda\) as \(n \rightarrow \infty\). (There is no guarantee that the MLE is an unbiased estimator; it just happens to be so here. Recall that the MLE will always be at least asymptotically unbiased, and it will always be a consistent estimator.)

If we wish to find the MLE for a function of the parameter, e.g., \(\lambda^2\), we simply apply that function to \(\hat{\theta}_{MLE}\). Hence \(\hat{\lambda^2}_{MLE}\) is \(\bar{X}^2\). This is the invariance property of the MLE.

Also, recall that the MLE converges in distribution to a normal random variable with mean \(\theta\) and variance \(1/I_n(\theta)\), where \(I_n(\theta)\) is the Fisher information content of the data sample. Here, that means that \[ \hat{\lambda} \stackrel{d}{\rightarrow} Y \sim \mathcal{N}\left(\lambda,\frac{\lambda}{n}\right) \,. \]

Recall: deriving the minimum variance unbiased estimator involves two steps:

1. factorizing the likelihood function to uncover a sufficient statistic \(U\) (that we assume is both minimal and complete); and
2. finding a function \(h(U)\) such that \(E[h(U)] = \lambda\).

A sufficient statistic for a parameter (or parameters) \(\theta\) captures all information about \(\theta\) contained in the sample.

The likelihood function is \[ \mathcal{L}(\lambda \vert \mathbf{x}) = \prod_{i=1}^n \frac{\lambda^{x_i}}{x_i!} e^{-\lambda} = \left(\prod_{i=1}^n \frac{1}{x_i!}\right) \left(\prod_{i=1}^n \lambda^{x_i}e^{-\lambda}\right) = \underbrace{\left(\prod_{i=1}^n \frac{1}{x_i!}\right)}_{h(\mathbf{x})} \underbrace{\lambda^{\sum_{i=1}^n x_i}e^{-n\lambda}}_{g\left(\sum_{i=1}^n x_i,\lambda\right)} \,. \] We see that a sufficient statistic is \(U = \sum_{i=1}^n X_i\). Let’s determine the expected value for \(U\): \[ E[U] = E\left[\sum_{i=1}^n X_i\right] = \sum_{i=1}^n E[X_i] = \sum_{i=1}^n \lambda = n\lambda \,. \] Thus \(h(U) = U/n = \bar{X}\) is the MVUE for \(\lambda\). As this matches the MLE, we know already that the MVUE is an unbiased (by definition) and consistent estimator. The next question is whether the variance of the MVUE achieves the Cramer-Rao Lower Bound on the variance of an unbiased estimator. We show that it does in an example below.

Note: the MVUE does not possess the invariance property, and it may be the case that it does not achieve the CRLB. Its primary advantage over the MLE is that the MVUE is the best estimator among those that are always unbiased, regardless of sample size.

---

The method of moments is a classic means by which to define estimators that has been historically useful when we are faced with the following situation: (a) the likelihood function is not easily differentiated, because it contains terms like \(\Gamma(\theta)\); and (b) the distribution has two or more free parameters, making it hard to define the MVUE (since we would have joint sufficient statistics). For instance, we face this situation when we work with the beta distribution from Chapter 3. But why do we say “historically useful”? Because in the age of computers, we can always determine MLEs numerically, using an optimization function. We will show an example of such a numerical computation below.

Recall that by definition, \(E[X^k]\) is the \(k^{\rm th}\) moment of the distribution of the random variable \(X\). We can define analagous sample moments, e.g., \[ m_1 = \frac{1}{n} \sum_{i=1}^n X_i = \bar{X} ~~ \mbox{and} ~~ m_2 = \frac{1}{n} \sum_{i=1}^n X_i^2 = \overline{X^2} \,. \] (For \(m_2\): note that the average of \(X_i^2\) is not the same as the average of \(X_i\), squared.) Let’s suppose that we have \(p\) parameters that we are trying to estimate. In method of moments estimation, we generally set the first \(p\) population moments equal to the first \(p\) sample moments and solve the system of equations to determine parameter estimates. These estimates are generally consistent, but also may be biased. (Situations may exist where higher-order moments may be preferable to use, such as when the one parameter of a distribution is \(\sigma^2\) and thus we might derive a better estimator using second moments, but typically we will use the first \(p\) moments.)

For the Poisson distribution, there is one parameter to estimate and thus we set \(\mu_1' = E[X] = \lambda = m_1' = \bar{X}\). We thus find that \(\hat{\lambda}_{MoM} = \bar{X}\). For a more relevant example of method of moments usage, see below.

---

4.5.1 Revisiting the Death-by-Horse-Kick Example

We begin this chapter by displaying the number of deaths per Prussian army corps per year resulting from horse kicks. Leaving aside the question of whether the data are truly Poisson distributed (a question we will try to answer later in this chapter), what is the estimated rate of death per corps per year?

The total number of events observed are \[ 0 \times 109 + 1 \times 65 + 2 \times 22 + 3 \times 3 + 4 \times 1 = 65 + 44 + 9 + 4 = 122 \,, \] and the total sample size is \(n = 200\), so \[ \hat{\lambda} = \bar{X} = \frac{1}{n} \sum_{i=1}^n X_i = \frac{122}{200} = 0.61 \,. \] This is the MLE, the MVUE, and the MoM estimate for \(\lambda\). In the next section, we will use these data to estimate a 95% confidence interval for \(\lambda\).

---

4.5.2 The CRLB on the Variance of \(\lambda\) Estimators

Recall: the Cramer-Rao Lower Bound (or CRLB) is the lower bound on the variance of any unbiased estimator. If an unbiased estimator achieves the CRLB, it is the MVUE…but it can be the case that the MVUE does not achieve the CRLB. For a discrete distribution, the CRLB is given by \[ V[\hat{\theta}] \geq -\left(nE\left[\frac{d^2}{d\theta^2} \log p_X(X \vert p) \right]\right)^{-1} = \frac{1}{nI(\theta)} \] where \(I(\theta)\) is the Fisher information.

For the Poisson distribution, \[\begin{align*} p_X(x \vert \lambda) &= \frac{\lambda^x}{x!}e^{-\lambda} \\ \log p_X(x \vert \lambda) &= x \log \lambda - \lambda - \log x! \\ \frac{d}{d\lambda} \log p_X(x \vert \lambda) &= \frac{x}{\lambda} - 1 \\ \frac{d^2}{d\lambda^2} \log p_X(x \vert \lambda) &= -\frac{x}{\lambda^2} \\ E \left[ \frac{d^2}{d\lambda^2} \log p_X(X \vert \lambda) \right] &= -\frac{1}{\lambda^2} E[X] \\ &= -\frac{1}{\lambda^2} \lambda = -\frac{1}{\lambda} \end{align*}\] and thus \[ V[\hat{\lambda}] \geq -\frac{1}{-n/\lambda} = \frac{\lambda}{n} \,. \] Thus \(\hat{\lambda}_{MLE}\), \(\hat{\lambda}_{MVUE}\), and \(\hat{\lambda}_{MoM}\) all achieve the CRLB.

---

4.5.3 Minimum Variance Unbiased Estimation and the Invariance Property

As stated above, the MVUE does not possess the property of invariance. To demonstrate the lack of invariance, we will define the MVUE for \(\lambda^2\).

The first thing to notice is that we cannot fall back on factorization to determine an appropriate sufficient statistic, since \(\lambda^2\) does not appear directly in the likelihood function. So we iterate: we make an initial guess and see where that guess takes us, and we guess again if our initial guess is wrong, etc.

An appropriate “guess” for \(\lambda^2\) is \(\bar{X}^2\): \[ E[\bar{X}^2] = V[\bar{X}] + (E[\bar{X}])^2 = \frac{\lambda}{n} + \lambda^2 \] We do get the term \(\lambda^2\) here…but we also get \(\lambda/n\). Hmm…so let’s try \(\bar{X}^2 - \bar{X}/n\) instead: \[ E\left[\bar{X}^2 - \frac{\bar{X}}{n}\right] = E[\bar{X}^2] - \frac{1}{n}E[\bar{X}] = \frac{\lambda}{n} + \lambda^2 - \frac{\lambda}{n} = \lambda^2 \,. \] Done! The MVUE for \(\lambda^2\) is thus \(\hat{\lambda^2}_{MVUE} = \bar{X}^2-\bar{X}/n\), which is not equal to \(\hat{\lambda^2}_{MLE} = \bar{X}^2\) (except in the limit \(n \rightarrow \infty\)).

---

4.5.4 Method of Moments Estimation for the Gamma Distribution

We will not officially introduce the gamma distribution until later in this chapter, but it is a good one to look at when exploring method of moments estimation. The probability density function for a gamma random variable \(X\) is \[ f_X(x) = \frac{x^{\alpha-1}}{\beta^{\alpha}} \frac{\exp(-x/\beta)}{\Gamma(\alpha)} \,, \] for \(x \geq 0\) and \(\alpha,\beta > 0\). The expected value is \(E[X] = \alpha \beta\) while the variance is \(V[X] = \alpha \beta^2\) (and thus \(E[X^2] = \alpha \beta^2 + \alpha^2 \beta^2\)).

Let’s assume we have \(n\) iid gamma-distributed random variables. Because there are two parameters, we match the first two moments: \[\begin{align*} \mu_1' = E[X] = \alpha \beta &= m_1' = \bar{X} \\ \mu_2' = E[X^2] = \alpha \beta^2 + \alpha^2 \beta^2 &= m_2' = \frac{1}{n}\sum_{i=1}^n X_i^2 = \overline{X^2} \,. \end{align*}\] Let \(\beta = \bar{X}/\alpha\). Then \[\begin{align*} \alpha \left( \frac{\bar{X}}{\alpha} \right)^2 + \alpha^2 \left( \frac{\bar{X}}{\alpha} \right)^2 &= \overline{X^2} \\ \frac{(\bar{X})^2}{\alpha} &= \overline{X^2} - (\bar{X})^2 \\ \Rightarrow ~~ \hat{\alpha}_{MoM} &= \frac{(\bar{X})^2}{\overline{X^2} - (\bar{X})^2} \,, \end{align*}\] and thus \[ \hat{\beta}_{MoM} = \frac{\bar{X}}{\hat{\alpha}_{MoM}} = \frac{\overline{X^2} - (\bar{X})^2}{\bar{X}} \,. \]

4.6 Confidence Intervals

Recall: a confidence interval is a random interval \([\hat{\theta}_L,\hat{\theta}_U]\) that overlaps (or covers) the true value \(\theta\) with probability \[ P\left( \hat{\theta}_L \leq \theta \leq \hat{\theta}_U \right) = 1 - \alpha \,, \] where \(1 - \alpha\) is the confidence coefficient. We determine \(\hat{\theta}\) by solving the following equation: \[ F_Y(y_{\rm obs} \vert \theta) - q = 0 \,, \] where \(F_Y(\cdot)\) is the cumulative distribution function for the statistic \(Y\), \(y_{\rm obs}\) is the observed value of the statistic, and \(q\) is an appropriate quantile value that is determined using the confidence interval reference table introduced in section 16 of Chapter 1.

As far as the construction of confidence intervals given a discrete sampling distribution goes, nothing changes algorithmically from where we were in Chapter 3; in an example below, we review how to construct such an interval for the Poisson parameter \(\lambda\).

---

In the context of statistical inference, there is one more important question to answer. What do we do if we neither know nor are willing to assume the distribution from which our data are sampled? Our root-finding algorithm relies upon knowing the sampling distribution of an observed statistic, and that in turn relies on knowing the distribution from which we draw each of our \(n\) iid data. One thing we can do is fall back upon bootstrapping. We demonstrate bootstrap confidence interval estimation in an example below.

---

4.6.1 Confidence Interval for the Poisson Parameter \(\lambda\)

Assume that we sample \(n\) iid data. We know that the sum \(Y = \sum_{i=1}^n X_i\) is a sufficient statistic for \(\lambda\) and that \(Y \sim\) Poisson(\(n\lambda\)). For this statistic, \(E[Y] = n\lambda\), which increases with \(\lambda\), so we know that we will utilize the “yes” lines of the confidence interval reference table. Our observed test statistic is \(y_{\rm obs} = \sum_{i=1}^n x_i\).

# Let's assume we observe ten years of data in a Poisson process
set.seed(101)
n      <- 10
lambda <- 8
X      <- rpois(n,lambda=lambda)

f <- function(nlambda,y.obs,q)
{
  ppois(y.obs,lambda=nlambda)-q
}
uniroot(f,interval=c(0.001,10000),y.obs=sum(X),1-alpha/2)$root/n

## [1] 5.810592

uniroot(f,interval=c(0.001,10000),y.obs=sum(X),alpha/2)$root/n

## [1] 9.178654

Note the division by \(n\) after the calls to uniroot(): this converts the interval bounds from being bounds on \(n\lambda\) to being bounds on \(\lambda\) itself. The interval is \([\hat{\lambda}_L,\hat{\lambda}_U] = [5.81,9.18]\), which overlaps the true value of 8. (See Figure 4.3.) Note that the interval over which we search for the root is [0.001,10000], which is (effectively) the range of possible values for \(\lambda\). (Recall that \(\lambda > 0\), hence the small but non-zero lower bound.)

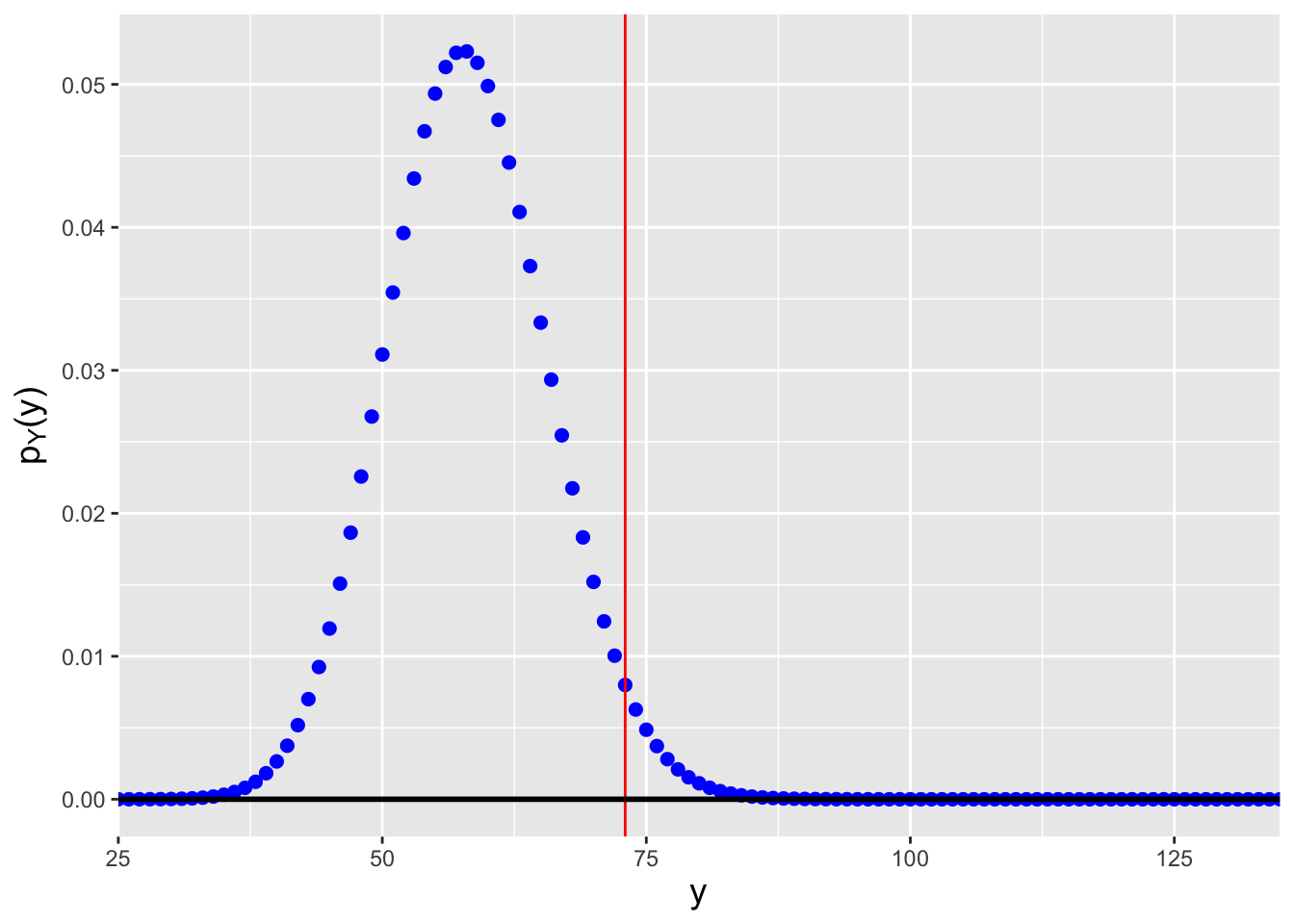
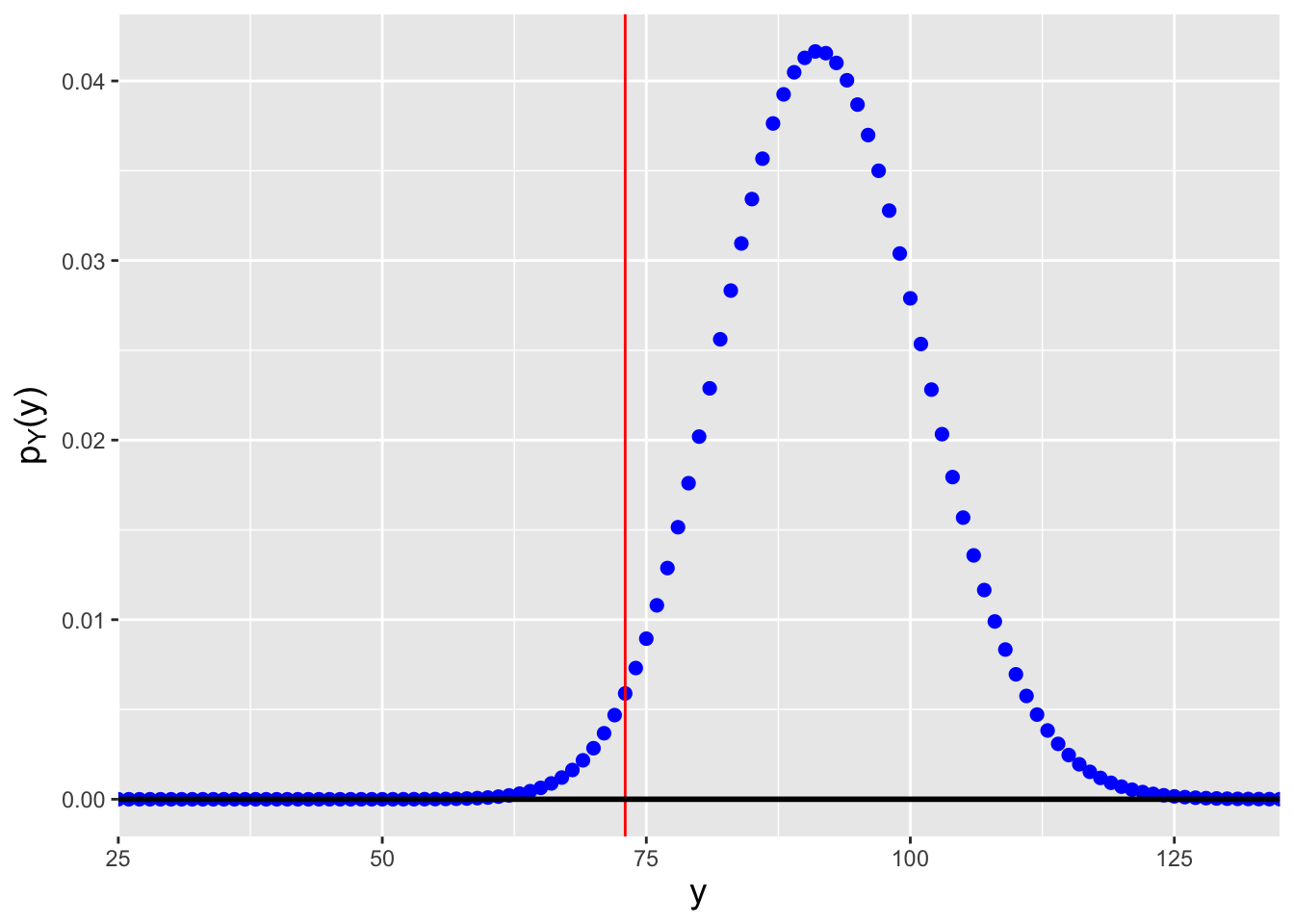
Figure 4.3: Probability mass functions for Poisson distributions for which (left) \(n\lambda=58.1\), and (right) \(n\lambda=91.8\). We assume that we observe \(y_{\rm obs} = \sum_{i=1}^n x_i = 73\) events in total and that we want to construct a 95% confidence interval for \(\lambda\). \(n\lambda=58.1\) is the smallest value of \(n\lambda\) such that \(F_Y^{-1}(0.975) = 73\), while \(n\lambda=91.8\) is the largest value of \(n\lambda\) such that \(F_Y^{-1}(0.025) = 73\).

In Chapter 3, we find that when we are constructing exact intervals with discrete sampling distributions (“exact” meaning that the sampling distribution is the correct one, not an approximation), the actual coverage can differ, either positively or negatively, from what we expect. This is a “discreteness effect” that goes away as the sample size \(n\) increases (i.e., as the discrete sampling distribution tends more and more to having a continuous appearance). Below, we compute the expected coverage for a two-sided interval, using the same approach we introduced in Chapter 3.

large <- 200
w.lo <- sum(ppois(0:large,lambda=n*lambda) < alpha/2)
alpha_over_2.lo.prime <- ppois(0:large,lambda=n*lambda)[w.lo]
w.hi <- sum(ppois(0:large,lambda=n*lambda) < 1-alpha/2)
alpha_over_2.hi.prime <- 1-ppois(0:(n*k),lambda=n*lambda)[w.hi]
round(100*(1-alpha_over_2.lo.prime-alpha_over_2.hi.prime),2)

## [1] 95

In this particular situation, the coverage actually is expected to be 95%!

---

4.6.2 Revisiting the Death-by-Horse-Kick Example

In the last section above, we determined that the rate of death from horse kicks per Prussian army corps per year was \(\hat{\lambda} = 0.61\). Here, we determine a 95% interval estimate for \(\lambda\).

X     <- c(rep(0,109),rep(1,65),rep(2,22),rep(3,3),rep(4,1))
n     <- length(X)
alpha <- 0.05

f <- function(nlambda,y.obs,q)
{
  ppois(y.obs,lambda=nlambda)-q
}
uniroot(f,interval=c(0.001,10000),y.obs=sum(X),1-alpha/2)$root/n

## [1] 0.5111252

uniroot(f,interval=c(0.001,10000),y.obs=sum(X),alpha/2)$root/n

## [1] 0.7283408

The 95% confidence interval is \([0.511,0.728]\).

---

4.6.3 Determining a Confidence Interval Using the Bootstrap

The bootstrap, invented by Bradley Efron in 1979, uses the observed data themselves to build up empirical sampling distributions for statistics. Let’s suppose we are handed the following data: \[ \mathbf{X} = \{X_1,X_2,\ldots,X_n\} \overset{iid}{\sim} P \,, \] where the distribution \(P\) is unknown. Now, let’s suppose further that from these data we compute a statistic: a single number. How can we build up an empirical sampling distribution from a single number? The answer is to repeatedly resample the data we observe, with replacement. For instance, if we have as data the numbers \(\{1,2,3\}\), a bootstrap sample might be \(\{1,1,3\}\) or \(\{2,3,3\}\), etc. Every time we resample the data, we compute the statistic we are interested in and record its value. Voila: we have an empirical sampling distribution. And if we can link the elements of that sampling distribution to a population parameter, we can immediately write down a confidence interval. For instance, if we have the \(n_{\rm boot}\) statistics \(\{\bar{X}_1,\ldots,\bar{X}_k\}\), we can put bounds on the population mean \(\mu\): \[\begin{align*} \hat{\mu}_L &= \bar{X}_{\alpha/2} \\ \hat{\mu}_U &= \bar{X}_{1-\alpha/2} \,, \end{align*}\] where \(\alpha/2\) and \(1-\alpha/2\) represent sample percentiles, e.g., the 2.5\(^{\rm th}\) and 97.5\(^{\rm th}\) percentiles.

Now, let’s assume we have the same data as in the first example above.

set.seed(101)
n      <- 10
lambda <- 8
X      <- rpois(n,lambda=lambda)
print(X)

##  [1] 7 4 9 9 6 6 8 7 9 8

The confidence interval that we construct for \(\lambda\), which is the distribution mean, is \([5.81,9.18]\). How does the bootstrap estimate of the mean compare?

n.boot <- 10000
x.bar  <- rep(NA,n.boot)
for ( ii in 1:n.boot ) {
  s         <- sample(length(X),length(X),replace=TRUE)
  x.bar[ii] <- mean(X[s])
}
quantile(x.bar,probs=c(0.025,0.975))

##  2.5% 97.5% 
##   6.3   8.2

The estimated interval is \([6.3,8.2]\). This is substantially smaller than what we found above, and that makes sense: for instance, the largest observed datum is 9, so the largest possible value of the bootstrap sample mean is 9…which is smaller than the previously determined upper bound of 9.18. What we are seeing is the effect of a small sample size: in the limit of small \(n\), the length of bootstrap confidence intervals is on average smaller than that of exact ones, with greater variability in lengths. As \(n\) increases, the mean lengths converge, but the variability in lengths remains larger for bootstrap intervals than for exact ones. What this means is that when we can propose a plausible distribution for our data, we should do so, as we will get more meaningful confidence intervals than if we were to fall back upon bootstrapping.

---

4.6.4 The Proportion of Observed Data in a Bootstrap Sample

Let’s assume that we sample \(n\) iid data from some distribution \(P\). When we create a bootstrap sample of these data, some of the observed data appear multiple times, while other data do not appear at all. What is the average proportion of observed data in any given bootstrap sample?

Let \(i\) be the index of an arbitrary datum, where the indices are \(\{1,2,\ldots,n-1,n\}\). Let \(X\) be the number of times \(i\) is chosen when we construct a bootstrap sample of size \(n\): \(X \sim\) Binom(\(n,1/n\)). \(P(X \geq 1)\) then represents the average proportion of observed data in a bootstrap sample: \[ P(X \geq 1) = 1 - P(X = 0) = 1 - (1-1/n)^n \,, \] which, as \(n \rightarrow \infty\), approaches \(1-1/e = 0.632\). Thus, for a sufficiently large sample, 63.2% of the observed data will appear at least once in a bootstrapped dataset.

4.7 Hypothesis Testing

Recall: a hypothesis test is a framework to make an inference about the value of a population parameter \(\theta\). The null hypothesis \(H_o\) is that \(\theta = \theta_o\), while possible alternatives \(H_a\) are \(\theta \neq \theta_o\) (two-tail test), \(\theta > \theta_o\) (upper-tail test), and \(\theta < \theta_o\) (lower-tail test). For, e.g., a one-tail test, we reject the null hypothesis if the observed test statistic \(y_{\rm obs}\) falls outside the bound given by \(y_{RR}\), which is a solution to the equation \[ F_Y(y_{RR} \vert \theta_o) - q = 0 \,, \] where \(F_Y(\cdot)\) is the cumulative distribution function for the statistic \(Y\) and \(q\) is an appropriate quantile value that is determined using the hypothesis test reference table introduced in section 17 of Chapter 1. Note that the hypothesis test framework only allows us to make a decision about a null hypothesis; nothing is proven.

In Chapter 3, we built upon the framework described above by introducing the Neyman-Pearson lemma. This result allows us to bypass the “guesswork” that goes into defining a hypothesis test statistic, by defining for us the most powerful test of a simple null hypothesis versus a simple specified alternative.

Recall: when we test the simple hypotheses \(H_o: \theta = \theta_o\) versus \(H_a: \theta = \theta_a\), the Neyman-Pearson lemma allows us to state that the hypothesis test with maximum power has a rejection region of the form \[ \frac{\mathcal{L}(\theta_o \vert \mathbf{x})}{\mathcal{L}(\theta_a \vert \mathbf{x})} < c(\alpha) \,, \] where \(c(\alpha)\) is a constant whose value depends on the specified Type I error \(\alpha\). In practice, we determine a sufficient statistic \(U\), and develop a hypothesis test as we have done previously using that statistic (or a function of it), assuming we know or can derive its sampling distribution. If the rejection region does not depend on \(\theta_a\), then the test is said to be a uniformly most powerful (UMP) test.

In an example, we demonstrate how to apply the NP lemma to construct a hypothesis test for the Poisson parameter \(\lambda\), given a sample of \(n\) iid data. Here we describe a more general hypothesis test framework, dubbed the likelihood ratio test (or LRT).

“Wait…the NP lemma had a likelihood ratio. How is the LRT different?”

That is a good question. It differs in how we specify the null and alternative hypotheses: \[ H_o: \theta \in \Theta_o ~~\mbox{vs.}~~ H_a: \theta \in \Theta_o^c \,, \] where \(\Theta_o\) (“capital theta naught”) represents a set of possible null values for \(\theta\), while \(\Theta_o^c\) is the complement of that set. For instance, for tests involving the Poisson parameter \(\lambda\), \(\Theta_o\) could be \(\lambda \in [5,10]\), so that \(\Theta_o^c\) is \(\lambda < 5\) or \(\lambda > 10\). (The null hypothesis in this example is a composite hypothesis, although it can be specified as a simple one, and usually is.) Let \(\Theta = \Theta_o \cup \Theta_o^c\), i.e., the union of the null and alternative sets. The rejection region for the LRT is \[ \lambda_{LR} = \frac{\mbox{sup}_{\theta \in \Theta_o} \mathcal{L}(\theta \vert \mathbf{x})}{\mbox{sup}_{\theta \in \Theta} \mathcal{L}(\theta \vert \mathbf{x})} < c(\alpha) \,, \] where, like it is in the context of the NP lemma, \(c(\alpha)\) is a constant that depends on the specified Type I error \(\alpha\).

“Since the LRT is more general, why would we ever utilize the NP lemma?”

That is another good question.

The primary point to make is that when we construct a test of two simple hypothesis within the framework of the NP lemma, we know that we are constructing the most powerful test of those hypotheses that we can construct. On the other hand, while the LRT is generally a powerful test, given the composite nature of one (or both) of the hypotheses it comes with no guarantee of being the most powerful test. (For instance, perhaps an alternative like the score test or the Wald test is the most powerful test in a given analysis situation.)

How does using the likelihood ratio test play out in practice? Let’s look at some possible use cases.

1. We have one freely varying parameter \(\theta\) and we wish to test \(H_o : \theta = \theta_o\) versus \(H_a : \theta \neq \theta_o\).

In this situation, we identify a sufficient statistic (or a function of it) for which we know the sampling distribution and use it to define a two-tail test as we have done previously, utilizing the hypothesis test reference tables.

2. We have one freely varying parameter \(\theta\) and we wish to define a one-sided alternative hypothesis, e.g., \(H_a : \theta < \theta_o\).

Here, the null hypothesis would be the complement of \(H_a\), i.e., \(H_o : \theta \geq \theta_o\). The distribution of the ratio \[ \lambda_{LR} = \frac{\mbox{sup}_{\theta \geq \theta_o} \mathcal{L}(\theta \vert \mathbf{x})}{\mathcal{L}(\hat{\theta}_{MLE} \vert \mathbf{x})} \] is thus not uniquely specifiable: it is a function of \(\theta\), and our null does not state a specific value for \(\theta\). So how would we determine \(y_{\rm RR}\)? It turns out the most conservative rejection-region boundary we can specify is the one that we would derive assuming that \(\theta = \theta_o\)…which means that to define an LRT, we would simply assume \(\theta_o\) as our null value, identify a sufficient statistic (or a function of it) for which we know the sampling distribution, and define a one-tail test as we have done previously.

3. We have two (or more) freely varying parameters.

In this context, we will have joint sufficient statistics that are sampled from a multivariate sampling distribution that may be difficult to work with directly. Thus we fall back upon Wilks’ theorem.

Let \(r_o\) denote the number of free parameters in \(H_o: \theta \in \Theta_o\) and let \(r\) denote the number of free parameters in \(\theta \in \Theta = \Theta_o \cup \Theta_a\). (To reiterate, \(\Theta\) must include all possible values of the parameters. For instance, if \(H_o\) is \(\theta = \theta_o\), then \(H_a\) must be \(\theta \neq \theta_o\) and not \(\theta < \theta_o\) or \(\theta > \theta_o\).) For large \(n\), \[ -2\log \lambda_{LR} \stackrel{d}{\rightarrow} W \sim \chi_{r-r_o}^2 \,, \] and we would reject the null hypothesis if \(-2\log \lambda_{LR} > w_{\rm RR} = F_{W(r-r_o)}^{-1}(1-\alpha)\). Since this result is related to the central limit theorem, large \(n\) would be, by rule-of-thumb, 30 or more.

---

4.7.1 The Uniformly Most Powerful Test of Poisson \(\lambda\)

Let’s say that we are counting the number of students that enter a classroom each minute. We assume that the entry of students is a homogeneous Poisson process (i.e., \(\lambda\), the expected number of entering students per time period, is constant). We think that five students, on average, will pass through the door each minute, while someone else thinks the number will be three. We collect data during five independent one-minute intervals: 4, 4, 3, 2, 3. Can we reject our null hypothesis at the level \(\alpha = 0.05\)? What is the \(p\)-value? And what is the power of the test for \(\lambda_a = 3\)?

We test the simple hypotheses \(H_o: \lambda_o = 5\) and \(H_a: \lambda_a = 3\). The factorized likelihood for our data sample is \[ \mathcal{L}(\lambda \vert \mathbf{x}) = \prod_{i=1}^n \frac{\lambda^{x_i}}{x_i!} e^{-\lambda} = \underbrace{\lambda^{\sum_{i=1}^n x_i} e^{-n\lambda}}_{g(\sum x_i,\lambda)} \cdot \underbrace{\frac{1}{\prod_{i=1}^n x_i!}}_{h(\mathbf{x})} \,. \] A sufficient statistic is thus \(Y = \sum_{i=1}^n X_i \sim\) Poisson(\(n\lambda\)). Since \(E[Y] = n\lambda\) increases with \(\lambda\), we find ourselves on the “yes” line of the hypothesis test reference tables, and specifically the “yes” line for a lower-tail test, and the rejection region is \(Y < y_{\rm RR} = F_Y^{-1}(\alpha \vert \lambda_o)\).

We determine \(y_{\rm RR}\) via the R function call y.rr <- qpois(alpha,lambda=n*lambda.o). Since \(y_{\rm obs} = 16\) and \(y_{\rm RR} = 17\), we reject the null hypothesis that \(\lambda = 5\). We can further write down that the \(p\)-value is ppois(y.obs,lambda=n*lambda.o), which is 0.038. (Note that since this is a lower-tail/yes test, we need not make a discreteness correction when computing either the \(p\)-value or the test power, i.e., we do not need to subtract 1 from y.obs in the function call above.) Since the rejection region does not depend on \(\lambda_a\), we have defined the uniformly most powerful test of \(\lambda_o\) versus \(\lambda_a\).

Thus far, the only way that we’ve utilized the alternative hypothesis \(H_a: \lambda_a = 3\) is when determining that we are conducting a lower-tail test. We will now use this value to determine the power of the test. The power is the probability of rejecting the null hypothesis given a specific value of \(\lambda\), i.e., \(P(Y < y_{\rm RR} \vert \lambda_a)\). Here, that value is given by ppois(y.lo,n*lambda.a), which is 0.664: if \(\lambda\) is truly equal to 3, we would reject the null hypothesis that \(\lambda_o = 5\) after collecting five data about two-thirds of the time.

---

4.7.2 Likelihood Ratio Test of the Poisson Parameter \(\lambda\)

Let’s assume the same setting as for the last example, but here, let’s say that we will test \(H_o: \lambda = \lambda_o = 5\) versus \(H_a: \lambda \neq \lambda_o\). The alternative hypothesis is a composite hypothesis, because it does not uniquely specify the shape of the probability mass function. Because we know the sampling distribution for the sufficient statistic \(Y = \sum_{i=1}^n X_i\) in the Poisson distribution with parameter \(n\lambda\), we can directly derive each of the two rejection region boundaries, which are \[\begin{align*} y_{\rm RR,lo} &= F_Y^{-1}(\alpha/2 \vert n\lambda_o)/n y_{\rm RR,hi} &= F_Y^{-1}(1-\alpha/2 \vert n\lambda_o)/n \,. \end{align*}\] In R, we determine the boundaries as y.rr.lo <- qpois(0.025,25), or 16, and y.rr.hi <- qpois(0.975,25), or 35. Our observed statistic is \(y_{\rm obs} = 16\), thus we fail to reject the null hypothesis.

As a reminder, because the alternative hypothesis is a composite hypothesis, the NP lemma does not apply here, and thus we cannot guarantee that the test we have just constructed is the most powerful of all possible tests of \(H_o: \lambda = \lambda_o\) versus \(H_a: \lambda \neq \lambda_o\).

---

4.7.3 Using Wilks’ Theorem to Test Hypotheses About the Normal Mean

We have collected \(n\) iid data from a normal distribution and we wish to test the hypothesis \(H_o: \mu = \mu_o\) versus the hypothesis \(H_a: \mu \neq \mu_o\) using the likelihood ratio test. (We assume the variance is unknown.)

For this problem, \[\begin{align*} \Theta_o &= \{ \mu,\sigma^2 : \mu = \mu_o, \sigma^2 > 0 \} \\ \Theta_a &= \{ \mu,\sigma^2 : \mu \neq \mu_o, \sigma^2 > 0 \} \,, \end{align*}\] and so \(\Theta = \Theta_o \cup \Theta_a = \{ \mu,\sigma^2 : \mu \in (-\infty,\infty), \sigma^2 > 0 \}\), with \(r_o = 1\) (\(\sigma^2\)) and \(r = 2\) (\(\mu,\sigma^2\)).

The likelihood for the normal pdf is \[ \mathcal{L}(\mu,\sigma \vert \mathbf{x}) = \prod_{i=1}^n \frac{1}{2 \pi \sigma^2} \exp\left( -\frac{(x_i-\mu)^2}{2\sigma^2} \right) \] and the log-likelihood is \[ \ell(\mu,\sigma \vert \mathbf{x}) = -\frac{n}{2} \log(2 \pi \sigma^2) - \frac{1}{2\sigma^2} \sum_{i=1}^n (x_i-\mu)^2 \,. \] The test statistic for Wilks’ theorem is \[ W = -2 \left[ \ell(\mu_o,\widehat{\sigma^2}_{MLE} \vert \mathbf{x}) - \ell(\hat{\mu}_{MLE},\widehat{\sigma^2}_{MLE} \vert \mathbf{x}) \right] \,, \] where \(\hat{\mu}_{MLE}\) and \(\widehat{\sigma^2}_{MLE}\) are the MLEs for \(\mu\) and \(\sigma\). We know these results from previous derivations: \[\begin{align*} \hat{\mu}_{MLE} &= \bar{X} \\ \widehat{\sigma^2}_{MLE} &= \frac{n-1}{n}S^2 = \frac{1}{n} \sum_{i=1}^n (X_i - \bar{X})^2 \,. \end{align*}\] (“Wait a second,” the reader says. “Shouldn’t we use \(\mu_o\) instead of \(\bar{X}\) for \(\widehat{\sigma^2}_{MLE}\) when optimizing the likelihood in the numerator above? In other words, shouldn’t we use \[ \widehat{\sigma^2}_{MLE,o} = \frac{1}{n} \sum_{i=1}^n (X_i - \mu_o)^2 \] instead of \(\widehat{\sigma^2}_{MLE}\)?” No, for the simple reason that \(\widehat{\sigma^2}_{MLE} \geq \widehat{\sigma^2}_{MLE,o}\): we achieve a “more likely” value of the distribution width when we center on where the data actually are, rather than where we hypothesize they are.) Ultimately, we compare the value of \(W\) against a chi-square distribution for \(r-r_o = 1\) degree of freedom, and thus we reject the null (at level \(\alpha = 0.05\)) if \(W > 3.841\) (= qchisq(0.95,1)).

---

4.7.4 Simulating the Likelihood Ratio Test

Wilks’ theorem generates an approximate result\(-\)it assumes that the test statistic is chi-square-distributed\(-\)and a major issue is that we do not know how good the approximation is. For instance, let’s say \(n = 20\)…this might be an insufficient sample size for the Wilks’ theorem machinery to yield an accurate and precise result (at least in terms of a rejection-region boundary).

To get a sense as to how well Wilks’ theorem works for us, we can run simulations. We simulate sets of data under the null (\(\mu = 5\)), and for each, we compute \(W\). The empirical rejection region boundary is then the, e.g., 95\(^{\rm th}\) percentile of the values of \(W\).

set.seed(101)

alpha   <- 0.05
num.sim <- 10000
n       <- 20
mu.o    <- 5      
sigma2  <- 9      # an arbitrary value
alpha   <- 0.05
W       <- rep(NA,num.sim)

f <- function(X,n,mu.o)
{
  hat.mu.mle     <- mean(X)
  hat.sigma2.mle <- (n-1)*var(X)/n

  logL.o <- -(n/2)*log(2*pi*hat.sigma2.mle)-(1/2/hat.sigma2.mle)*sum((X-mu.o)^2)
  logL   <- -(n/2)*log(2*pi*hat.sigma2.mle)-(1/2/hat.sigma2.mle)*sum((X-hat.mu.mle)^2)
  return(-2*(logL.o - logL))
}

for ( ii in 1:num.sim ) {
  X     <- rnorm(n,mean=mu.o,sd=sqrt(sigma2))
  W[ii] <- f(X,n,mu.o)
}

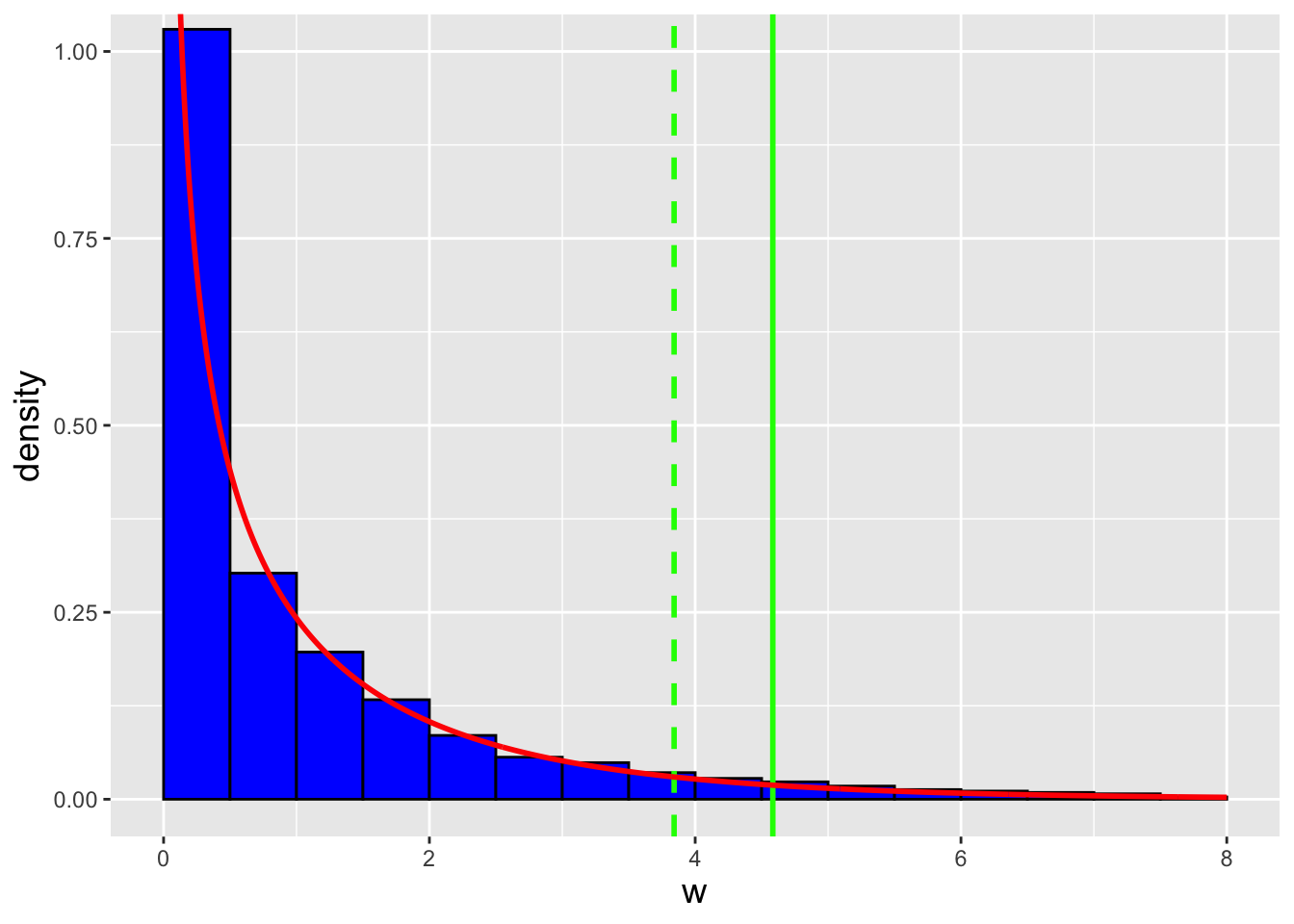
Figure 4.4: The empirical distribution of the statistic \(-2(\log\mathcal{L}_o - \log\mathcal{L}_a)\), with the chi-square distribution for \(\Delta r = 1\) degree of freedom overlaid (red curve). The dashed vertical green line represents the rejection region boundary according to Wilks’ theorem, and the solid vertical green line represents the 95th percentile of simulated statistic values. The divergence of the two green lines indicates that Wilks’ theorem at best provides approximate results and that simulations can provide more accurate and precise results.

In this simulation, we find that the empirical rejection-region boundary is 4.584, which is sufficiently far from the value 3.841 derived from Wilks’ theorem to be concerning. We also find that if we adopt 3.841 as our boundary value, our Type I error is actually 0.071 instead of the expected value of 0.05. The upshot: if \(n\) is small, it is best not to assume that \(W\) is chi-square-distributed; run simulations to determine rejection region boundaries and \(p\)-values instead.

4.8 The Gamma Distribution

The gamma distribution is a continuous distribution that is commonly used to, e.g., model the waiting times between discrete events. Its probability density function is given by \[ f_X(x) = \frac{x^{\alpha-1}}{\beta^\alpha} \frac{\exp\left(-x/\beta\right)}{\Gamma(\alpha)} \,, \] where \(x \in [0,\infty)\), \(\alpha\) and \(\beta\) are both \(>\) 0, and \(\Gamma(\alpha)\) is the gamma function: \[ \Gamma(\alpha) = \int_0^\infty u^{\alpha-1} e^{-u} du \,. \] (See Figure 4.5.) \(\alpha\) and \(\beta\) are referred to as “shape” and “scale” parameters, respectively. The gamma family of distributions exhibits a wide variety of functional shapes and it is the parent family to a number of other distributions, some of which we have met before. One in particular is the exponential distribution, \[ f_X(x) = \frac{1}{\beta} \exp\left(-\frac{x}{\beta}\right) \,, \] which is a gamma distribution with \(\alpha = 1\). Note how we lead off above by saying that the gamma distribution is commonly used to model the waiting times between discrete events. The exponential distribution specifically models the waiting time between one event and the next in a Poisson process. The number of strong earthquakes that occur in California in one year? That can be modeled as a Poisson random variable. The time that elapses between two consecutive strong earthquakes in California? That can be modeled using the exponential distribution. (For completeness: the Erlang distribution is a generalization of the exponential distribution, in the sense that we can use it to model the waiting time between the \(i^{\rm th}\) and \((i+\alpha)^{\rm th}\) events, where \(\alpha\) is a positive integer, in a Poisson process.)

Distributions Within the Gamma Family of Distributions

distribution	\(\alpha\)	\(\beta\)
exponential	1	\((0,\infty)\)
Erlang	\(\{1,2,3,\ldots\}\)	\((0,\infty)\)
chi-square	\(\{1/2,1,3/2,\ldots\}\)	2

Let’s conclude this section by repeating the exercise we did in the last chapter while discussing the beta distribution, the one in which we examined the functional form of the likelihood function \(\mathcal{L}(p \vert k,x)\). Here, we write down the Poisson likelihood function \[ \mathcal{L}(\lambda \vert x) = \frac{\lambda^x}{x!} e^{-\lambda} \] and compare it with the gamma pdf. We can match the gamma pdf if we map the Poisson \(\lambda\) to the gamma \(x\), the Poisson \(x\) to the gamma \(\alpha-1\), and we set \(\beta\) to 1. But because the Poisson \(x\) is an integer with values \(\{0,1,2,\ldots\}\), we find that the integrand specifically matches the Erlang pdf, for which \(\alpha = \{1,2,3,\ldots\}\). So, if we observe a random variable \(X \sim\) Poisson(\(\lambda\)), then the likelihood function \(\mathcal{L}(\lambda \vert x)\) has the shape (and normalization!) of a Gamma(\(x+1,1\)) (or Erlang(\(x+1\))) distribution.

(About the normalization: if we integrate the likelihood function over its domain, we find that \[ \frac{1}{x!} \int_0^\infty \lambda^x e^{-\lambda} d\lambda = \frac{1}{x!} \Gamma(x+1) = \frac{x!}{x!} = 1 \,. \] The mathematics works out because \(x\) is integer valued and thus \(\Gamma(x+1) = x!\).)

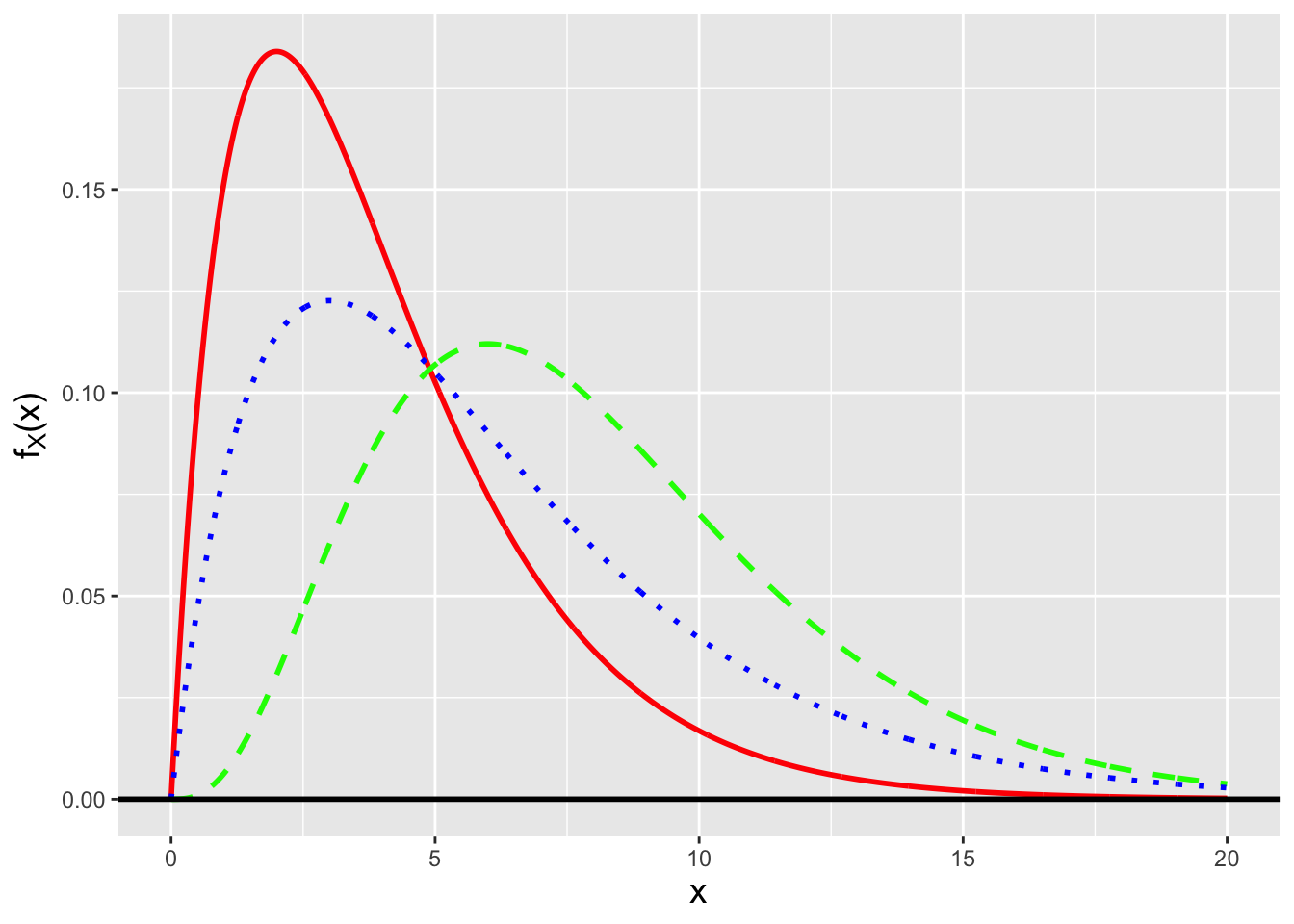
Figure 4.5: Three examples of gamma probability density functions: Gamma(2,2) (solid red line), Gamma(4,2) (dashed green line), and Gamma(2,3) (dotted blue line).

---

4.8.1 The Expected Value of a Gamma Random Variable

The expected value of a gamma random variable is found by introducing constants into the expected value integral so that a gamma pdf integrand is formed. Specifically \[\begin{align*} E[X] = \int_0^\infty x f_X(x) dx &= \int_0^\infty x \frac{x^{\alpha-1}}{\beta^\alpha} \frac{\exp(-x/\beta)}{\Gamma(\alpha)} dx \\ &= \int_0^\infty \frac{x^{\alpha}}{\beta^\alpha} \frac{\exp(-x/\beta)}{\Gamma(\alpha)} dx \\ &= \int_0^\infty \frac{x^{\alpha}}{\beta^\alpha} \frac{\exp(-x/\beta)}{\Gamma(\alpha)} \frac{\Gamma(\alpha+1)}{\Gamma(\alpha+1)} \frac{\beta^{\alpha+1}}{\beta^{\alpha+1}} dx \\ &= \int_0^\infty \frac{x^{\alpha}}{\beta^{\alpha+1}} \frac{\exp(-x/\beta)}{\Gamma(\alpha+1)} \frac{\Gamma(\alpha+1)}{\Gamma(\alpha)} \frac{\beta^{\alpha+1}}{\beta^\alpha} dx \\ &= \frac{\Gamma(\alpha+1)}{\Gamma(\alpha)} \frac{\beta^{\alpha+1}}{\beta^\alpha} \int_0^\infty \frac{x^{\alpha}}{\beta^{\alpha+1}} \frac{\exp(-x/\beta)}{\Gamma(\alpha+1)} dx \\ &= \frac{\alpha \Gamma(\alpha)}{\Gamma(\alpha)} \beta \times 1 \\ &= \alpha \beta \,. \end{align*}\] By introducing the constants, we are able to transform the integrand to that of a Gamma(\(\alpha+1,\beta\)) distribution, and because the integral is over the entire domain of a gamma distribution, the integral evaluates to 1.

A similar calculation involving the derivation of \(E[X^2]\) allows us to determine that the variance of a gamma random variable is \(V[X] = \alpha \beta^2\).

---

4.8.2 The Distribution of the Sum of Exponential Random Variables

As stated above, the exponential distribution, i.e., the gamma distribution with \(\alpha = 1\), is used to model the waiting time between two successive events in a Poisson process. Let’s assume that we have recorded \(n\) separate times between \(n\) separate pairs of events. What is the distribution of \(T = T_1 + \cdots + T_n\)?

As we do when faced with a linear function of \(n\) iid random variables, we utilize the method of moment-generating functions: \[ m_T(t) = \prod_{i=1}^n m_{T_i}(t) \,, \] where \(m_{T_i}(t) = (1-\beta t)^{-1}\) is the mgf for the exponential distribution. Thus \[ m_T(t) = \prod_{i=1}^n (1-\beta t)^{-1} = (1-\beta t)^{-n} \,. \] This has the form of the mgf for a Gamma(\(n,\beta\)) distribution, or, equivalently, an Erlang(\(n,\beta\)) distribution. In other words the sum of \(n\) iid waiting times has the same distribution as the waiting time between the \(i^{\rm th}\) and \((i+n)^{\rm th}\) events of a Poisson process.

---

4.8.3 Memorylessness and the Exponential Distribution

An important feature of the exponential distribution is that when we use it to model, e.g., the lifetimes of components in a system, it exhibits memorylessness. In other words, if \(T\) is the random variable representing a component’s lifetime, where \(T \sim\) Exponential(\(\beta\)) and where \(E[T] = \beta\), it doesn’t matter how old the component is when we first examine it: from that point onward, the average lifetime will be \(\beta\).

Let’s demonstrate how this works. We examine a component “born” at time \(t_0=0\) at a later time \(t_1\), and we wish to determine the probability that it will live beyond an even later time \(t_2\). In other words, we wish to compute \[ P(T \geq t_2-t_0 \vert T \geq t_1-t_0) \,. \] (We know the component lived to time \(t_1\), hence the added condition.) Let \(T \sim\) Exponential(\(\beta\)). Then \[\begin{align*} P(T \geq t_2-t_0 \vert T \geq t_1-t_0) &= \frac{P(T \geq t_2-t_0 \cap T \geq t_1-t_0)}{P(T \geq t_1-t_0)} \\ &= \frac{P(T \geq t_2-t_0)}{P(T \geq t_1-t_0)} \\ &= \frac{\int_{t_2-t_0}^\infty (1/\beta) \exp(-t/\beta) dt}{\int_{t_1-t_0}^\infty (1/\beta) \exp(-t/\beta) dt} \\ &= \frac{\left. -\exp(-t/\beta) \right|_{t_2-t_0}^\infty}{\left. -\exp(-t/\beta) \right|_{t_1-t_0}^\infty} \\ &= \frac{0 + \exp(-(t_2-t_0)/\beta)}{0 + \exp(-(t_1-t_0)/\beta)} \\ &= \exp[-(t_2-t_1)/\beta] = P(T \geq t_2-t_1) \,. \end{align*}\] Note that \(t_0\) drops out of the final result: no matter how long ago \(t_0\) might have been, the probability that the component will live \(t_2-t_1\) units longer is the same, and the average additional lifetime is still \(\beta\).

4.9 Poisson Regression

Suppose that for a given measurement \(x\), we record a random variable \(Y\) that is a number of counts. For instance, \(x\) might be the time of day, and \(Y\) might be the observed number of cars parked in a lot at that time. Because \(Y\) is (a) integer valued, and (b) non-negative, an appropriate distribution for the random variable \(Y \vert x\) might be the Poisson distribution, and thus to model these data, we may want to pursue the use of Poisson regression.

Recall: To implement a generalized linear model (or GLM), we need to do two things:

1. examine the \(Y_i\) values and select an appropriate distribution for them (discrete or continuous? what is the functional domain?); and
2. define a link function \(g(\theta \vert x)\) that maps the line \(\beta_0 + \beta_1 x_i\), which has infinite range, into a more limited range (e.g., \([0,\infty)\)).

Because \(\lambda > 0\), in Poisson regression we adopt a link function that maps \(\beta_0 + \beta_1 x\) from the range \((-\infty,\infty)\) to \((0,\infty)\). There is no unique choice of link function, but the conventionally applied one is the logarithm: \[ g(\lambda \vert x) = \log (\lambda \vert x) = \beta_0 + \beta_1 x ~~\implies~~ \lambda \vert x = e^{\beta_0 + \beta_1 x} \,. \] Similar to logistic regression, our goal is to estimate \(\beta_0\) and \(\beta_1\), which is done via numerical optimization of the likelihood function \[ \mathcal{L}(\beta_0,\beta_1 \vert \mathbf{y}) = \prod_{i=1}^n p_{Y \vert \beta_0,\beta_1}(y_i \vert \beta_0,\beta_1) = \prod_{i=1}^n \frac{\exp(\beta_0+\beta_1x_i)^{x_i}}{x_i!} e^{-\exp(\beta_0+\beta_1x_i)} \,. \]

---

For the Poisson distribution, \(E[X] = V[X] = \lambda\), so the expectation is that for any given value \(x\), \(E[Y \vert x] = V[Y \vert x]\). However, it is commonly seen in real-life data that the sample variance of \(Y \vert x\) exceeds the sample mean. This is dubbed overdispersion, and it can arise when, e.g., the observed Poisson process is inhomogeneous…or differently stated, when \(\lambda\) varies as a function of space and/or time. A standard way to deal with overdispersion is to move from Poisson regression to negative binomial regression.

Before we say more…we note that while the name “negative binomial regression” is technically correct (in the sense that the model assumes that the response data are negative binomially distributed), it can be very confusing for those new to regression, who might view the negative binomial as a distribution that is only useful when, e.g., modeling failures in Bernoulli trials. How could that distribution possibly apply here? The answer is that the negative binomial probability mass function is “just” a function (and as such, it is “allowed” to have more general use than just modeling failures), but more to the point, it is a function that arises naturally when we apply the Law of Total Probability to the Poisson pmf.

Let’s suppose that \(Y \vert x \sim\) Poisson(\(\lambda\)), but that \(\lambda\) itself is a random variable. There is no unique way to model the distribution of \(\lambda\), but the gamma distribution provides a flexible means by which to do so (since the family encompasses a wide variety of shapes, unlike, say, the normal distribution, which can never be skew). Let’s assume that \(\lambda \sim\) Gamma(\(\theta,p/\theta\)). The distribution of \(Y\) is found with the LoTP: \[\begin{align*} p_{Y \vert \theta,p}(y \vert \theta,p) &= \int_0^\infty p_{Y \vert \lambda}(y \vert \lambda) f_{\lambda}(\lambda \vert \theta,p) d\lambda \\ &= \int_0^\infty \frac{\lambda^y}{y!} e^{-\lambda} \frac{\lambda^{\theta-1}}{(p/\theta)^\theta} \frac{e^{-\lambda/(p/\theta)}}{\Gamma(\theta)} d\lambda \\ &= \frac{1}{y!}\left(\frac{\theta}{p}\right)^\theta \frac{1}{\Gamma(\theta)} \int_0^\infty \lambda^{y+\theta+1} e^{-\lambda(1+\theta/p)} d\lambda \,. \end{align*}\] The integrand looks suspiciously like the integrand of a gamma function integral, but we have to change \(\lambda(1+\theta/p)\) in the exponential to just \(\lambda'\): \[ \lambda' = \lambda(1+\theta/p) ~~ \mbox{and} ~~ d\lambda' = d\lambda (1+\theta/p) \,. \] The bounds of the integral do not change. The integral now becomes \[\begin{align*} p_{Y \vert \theta,p}(y \vert \theta,p) &= \frac{1}{y!}\left(\frac{\theta}{p}\right)^\theta \frac{1}{\Gamma(\theta)} \frac{1}{(1+\theta/p)^{y+\theta}} \int_0^\infty (\lambda')^{y+\theta-1} e^{-\lambda'} d\lambda' \\ &= \frac{1}{y!}\left(\frac{\theta}{p}\right)^\theta \frac{1}{\Gamma(\theta)} \frac{1}{(1+\theta/p)^{y+\theta}} \Gamma(y+\theta) \\ &= \frac{(y+\theta-1)!}{y! (\theta-1)!} \left(\frac{\theta}{p}\right)^\theta \left(\frac{p}{p+\theta}\right)^{y+\theta} \\ &= \binom{y+\theta-1}{y} \left(\frac{p}{p+\theta}\right)^y \left(\frac{\theta}{p}\right)^\theta \left(\frac{p}{p+\theta}\right)^\theta \\ &= \binom{y+\theta-1}{y} \left(\frac{p}{p+\theta}\right)^y \left(\frac{\theta}{p+\theta}\right)^\theta \\ &= \binom{y+\theta-1}{y} \left(\frac{\theta}{p+\theta}\right)^\theta \left(1 - \frac{\theta}{p+\theta}\right)^y \,. \end{align*}\] This has the functional form of a negative binomial pmf in which \(y\) represents the number of “failures,” \(\theta\) is the number of “successes,” and \(\theta/(p+\theta)\) is the probability of success.

Now, why do we choose this form of the negative binomial distribution? We do so because it so happens that \[\begin{align*} E[Y] &= p \\ V[Y] &= p + \frac{p^2}{\theta} \,. \end{align*}\] (One can derive these quantities starting with, e.g., \(E[Y] = \theta(1-p')/p'\) and \(V[Y] = \theta(1-p')/(p')^2\) and plugging in \(p' = \theta/(p+\theta)\).) Varying \(\theta\) thus allows us to model the overdispersion with a single variable. (We assume that \(p\) takes the place of \(\lambda\), in the sense that now \(p \vert x = \exp(\beta_0 + \beta_1x\)).) In the limit that \(\theta \rightarrow \infty\), negative binomial regression becomes Poisson regression. Because the overdispersion is represented in a single variable, we can examine the results of learning both Poisson and negative binomial regression models to determine whether or not the quality of fit improves enough to justify the extra model complexity.

---

4.9.1 Revisiting the Death-by-Horse-Kick Example

Modeling Bortkiewicz’s horse-kick dataset provides a simple example of the use of Poisson regression.

x <- 0:4
Y <- c(109,65,22,3,1)

poi.out <- glm(Y~x,family=poisson)
summary(poi.out)

## 
## Call:
## glm(formula = Y ~ x, family = poisson)
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  4.80136    0.08490   56.55   <2e-16 ***
## x           -0.92213    0.07704  -11.97   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 232.430  on 4  degrees of freedom
## Residual deviance:  12.437  on 3  degrees of freedom
## AIC: 38.911
## 
## Number of Fisher Scoring iterations: 5

The summary output from the Poisson regression model is, in its structure, identical to that of logistic regression. But there are some differences in how values are defined. For instance, the deviance residual is \[ d_i = \mbox{sign}(Y_i - \hat{Y}_i) \sqrt{2[Y_i \log (Y_i/\hat{Y}_i) - (Y_i - \hat{Y}_i)]} \,, \] where \[ \hat{Y}_i = \hat{\lambda}_i = \exp(\hat{\beta}_0+\hat{\beta}_1 x_i) \,. \] (Note that when \(Y_i = 0\), \(Y_i \log (Y_i/\hat{Y}_i)\) is assumed to be zero.) Because there are only five data points in the fit, all the deviance residual values are displayed, rather than a five-number summary. Also, the residual deviance (here, 12.437) is not \(-2 \log \mathcal{L}_{max}\), as it was for logistic regression. There are two ways to determine \(\mathcal{L}_{max}\); one is to take the AIC value (38.911), subtract 2 times the number of model terms (2 here, thus yielding 34.911), and then dividing by \(-2\). The more straightforward way, however, is to utilize the logLik() function:

logLik(poi.out)

## 'log Lik.' -17.45551 (df=2)

As we did in the context of logistic regression, we can use the the difference in the values of the null and residual deviances (here, 232.430-12.437 = 219.993) to test the null hypothesis that \(\beta_1 = 0\). The difference is assumed to be sampled from a chi-square distribution for 4-3 = 1 degree of freedom. The \(p\)-value is 1 - pchisq(220.0,1) or effectively zero: we emphatically reject the null hypothesis that \(\beta_1 = 0\).

As a final note, unlike the case of logistic regression where determining the quality of fit of the learned model is not particularly straightforward, for Poisson regression we can simply assume that the residual deviance is chi-square-distributed for the given number of degrees of freedom. Here, the \(p\)-value is

1 - pchisq(12.437,3)

## [1] 0.006026712

or 0.0060. Because this value is less than, e.g., \(\alpha = 0.05\), we would (in this instance) reject the null hypothesis that the observed data are truly Poisson distributed.

---

4.9.2 Negative Binomial Regression Example

In the code chunk below, we simulate 100 data at each of four different values of \(x\): 1, 2, 3, and 4. The data are simulated with a Poisson overdispersion factor of 2.

set.seed(236)
n <- 100               # 100 data per x value
x <- rep(c(1,2,3,4),n)
Y <- rep(NA,length(x))
for ( ii in 1:length(x) ) {
  Y[ii] <- rpois(1,rgamma(1,2,scale=x[ii]/2))
}

For these data, \(E[Y \vert x] = x\) and \(V[Y \vert x] = x + x^2/2\), meaning that the overdispersion factor is, again, \(\theta = 2\). Let’s see how overdispersion affects the learning of a Poisson regression model.

First, the Poisson regression model itself:

summary(glm(Y~x,family=poisson))

## 
## Call:
## glm(formula = Y ~ x, family = poisson)
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -0.08336    0.09240  -0.902    0.367    
## x            0.38014    0.02944  12.913   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 1107  on 399  degrees of freedom
## Residual deviance:  930  on 398  degrees of freedom
## AIC: 1805
## 
## Number of Fisher Scoring iterations: 5

…and second, the negative binomial regression model, as learned using the glm.nb() function of the MASS package. (Note that MASS does not represent the state of Massachusetts, but rather stands for “Modern Applied Statistics with S”…with S being the precursor software to R.)

library(MASS)
summary(glm.nb(Y~x))

## 
## Call:
## glm.nb(formula = Y ~ x, init.theta = 1.84882707, link = log)
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -0.10769    0.13101  -0.822    0.411    
## x            0.38908    0.04483   8.679   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Negative Binomial(1.8488) family taken to be 1)
## 
##     Null deviance: 530.52  on 399  degrees of freedom
## Residual deviance: 454.45  on 398  degrees of freedom
## AIC: 1633.9
## 
## Number of Fisher Scoring iterations: 1
## 
## 
##               Theta:  1.849 
##           Std. Err.:  0.258 
## 
##  2 x log-likelihood:  -1627.868

The negative binomial model is displayed in Figure 4.6. When we compare the output, we first look for the lines beginning with AIC:

AIC: 1805    [Poisson regression]
AIC: 1633.9  [negative binomial regression]

The Akaike Information Criterion, or AIC, as we will recall, is a quality-of-fit metric that penalizes model complexity. If we learn a suite of models, we would generally adopt that associated with the lowest AIC value. Here, the negative binomial model has a much lower AIC value than the Poisson model, so we would definitely adopt it! But is the negative binomial model a good model in an absolute sense? To determine that, we would compare the residual deviance value of 454.45 against a chi-square distribution with 398 degrees of freedom; the result is

1 - pchisq(454.45,398) = 0.026

We would reject the null hypothesis that the negative binomial model is the correct representation of the data-generating process, but we note that the \(p\)-value is only slightly smaller than 0.05: the model may not be technically “correct,” but it appears to be at least approximately correct!

The estimated value of the overdispersion parameter is \(\hat{\theta} = 1.849\), with estimated standard error \(0.258\). This is consistent with the true value \(\theta = 2\) and is definitely inconsistent with \(\theta = \infty\) (the value for truly Poisson-distributed data). (Note that when the data are not overdispersed, \(\hat{\theta}\) will usually be a large number, but not actually infinity.)

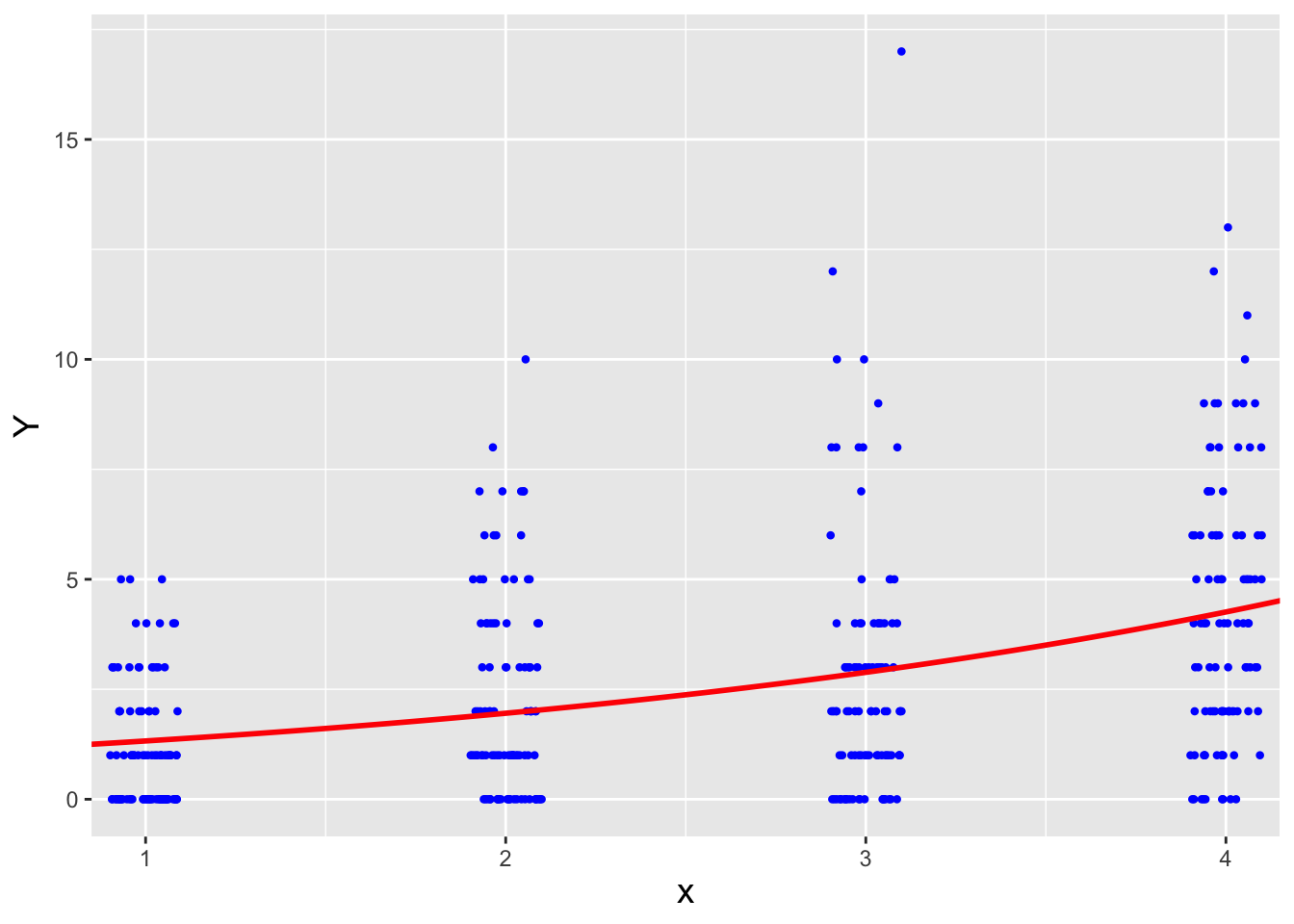
Figure 4.6: The negative binomial regression line superimposed on the simulated data. The jitter() function is applied to the \(x\) values to allow us to more easily see the number of counts as a function of \(x\) and \(Y\).

4.10 Chi-Square-Based Hypothesis Testing

In the previous chapter, we introduced the chi-square goodness-of-fit test as a way of conducting hypothesis tests given multinomial data. Given \(k\) data recorded in \(m\) separate bins, we can compute the test statistic \[ W = \sum_{i=1}^m \frac{(X_i - kp_i)^2}{kp_i} \,, \] where \(X_i\) is the number of data observed in bin \(i\), and where \(p_i\) is the probability of any one datum being observed in that bin under the null. If \(k\) is sufficiently large, then \(W\) converges in distribution to a chi-square random variable for \(m-1\) degrees of freedom. (Hence the name of the test!)

But: what if the overall observed number of data \(X\) is a random variable instead of being a set constant \(X=k\)? Imagine a very simple digital camera that has four light collecting bins, each of the same size, and we point it towards a light source that emits an average of \(\lambda\) photons in a particular time period. If we open the shutter for that time period, what we would observe is \(X \sim\) Poisson(\(\lambda\)) photons, with the numbers in each bin being \(\{X_1,X_2,X_3,X_4\}\). Now let’s say we want to test the hypothesis that the probability of a photon falling into each bin is the same, i.e., \(H_o: p_1 = p_2 = p_3 = p_4 = 1/4\). If we were to use the chi-square GoF test directly, we would compute \[ w_{obs} = \sum_{i=1}^4 \frac{(X_i - \lambda p_i)^2}{\lambda p_i} \] and then compute the \(p\)-value \(1-F_W(w_{obs})\) assume 3 degrees of freedom. (In R, this would be computed via 1 - pchisq(w.obs,3).) We can do this\(-\)the computer will not stop us from doing so\(-\)but is this valid?

The answer is that this is valid so long as each \(X_i\) converges in distribution to a normal random variable. And Poisson random variables do converge in distribution to normal random variables. Thus, in short, yes, use of the chi-square GoF test is valid if \(\lambda p_i\) is large. The question is, how large?

---

The Poisson probability mass function is \[ p_X(x \vert \lambda) = \frac{\lambda^x}{x!} e^{-\lambda} \,. \] We note that the normal probability density function does not have a factorial in it, so we will start by using Stirling’s approximation: \[ x! \approx \sqrt{2 \pi x} x^x e^{-x} \,. \] This approximation has an error of 1.65% for \(x = 5\) and 0.83% for \(x = 10\), with the percentage error continuing to shrink as \(x \rightarrow \infty\). With this approximation, we can write that \[ p_X(x \vert \lambda) \approx \frac{\lambda^x}{\sqrt{2 \pi x}} x^{-x} e^{x-\lambda} \,. \] This still does not quite look like a normal pdf. So there is more work to do. We compute the logarithm of this quantity: \[ \log p_X(x \vert \lambda) \approx x \log \lambda - \frac{1}{2} \log (2 \pi x) - x \log x + x - \lambda = -x ( \log x - \log \lambda ) - \frac{1}{2} \log (2 \pi x) + x - \lambda \,, \] and then look at \(\log x - \log \lambda\): \[ \log x - \log \lambda = \log \frac{x}{\lambda} = \log \left( 1 - \frac{\lambda-x}{\lambda}\right) \approx -\frac{\delta}{\sqrt{\lambda}} - \frac{\delta^2}{2 \lambda} - \cdots \,. \] Here, \(\delta = (\lambda - x)/\sqrt{\lambda}\). Plugging this result into the expression for \(\log p_X(x \vert \lambda)\), we find that \[ \log p_X(x \vert \lambda) \approx -\frac{1}{2} \log (2 \pi x) + x \left( \frac{\delta}{\sqrt{\lambda}} + \frac{\delta^2}{2\lambda} \right) - \delta \sqrt{\lambda} \,. \] The next step is plug in \(x = \lambda - \sqrt{\lambda}\delta\): \[\begin{align*} \log p_X(x \vert \lambda) &\approx -\frac{1}{2} \log (2 \pi x) + (\lambda - \sqrt{\lambda}\delta)\left( \frac{\delta}{\sqrt{\lambda}} + \frac{\delta^2}{2\lambda} \right) - \delta \sqrt{\lambda} \\ &= -\frac{1}{2} \log (2 \pi x) + \sqrt{\lambda}\delta - \delta^2 + \frac{\delta^2}{2} - \frac{\delta^3}{2 \lambda^{3/2}} - \sqrt{\lambda}\delta \\ &\approx -\frac{1}{2} \log (2 \pi x) - \frac{\delta^2}{2} \,, \end{align*}\] where we drop the \(\mathcal{O}(\delta^3)\) term. When we exponentiate both sides, the final result is \[ p_X(x \vert \lambda) \approx \frac{1}{\sqrt{2 \pi x}} \exp\left( -\frac{\delta^2}{2} \right) = \frac{1}{\sqrt{2 \pi x}} \exp\left( -\frac{(x-\lambda)^2}{2\sqrt{\lambda}} \right) \,. \] This has the (approximate) form of a normal pdf, at least for values \(x \approx \lambda\). So, in the end, the Poisson probability mass function \(p_X(x \vert \lambda)\) has approximately the same shape as the normal probability density function \(f_X(x \vert \mu=\lambda,\sigma^2=\lambda)\) for \(x \gg 1\) and \(x \approx \lambda\).

The conventional rule-of-thumb is that one can utilize the chi-square GoF test with Poisson data so long as \(\lambda p_i \geq 5\) counts in each bin.

---

4.10.1 Revisiting the Death-by-Horse-Kick Example

In previous examples, we have shown that over the course of 20 years, in 10 separate Prussian army corps, soldiers died as a result of horse kicks at a rate of \(\hat{\lambda} = \bar{X} = 0.61\) deaths per corps per year, and that a 95% confidence interval for \(\lambda\) is [0.51,0.73]. However, we never examined what is perhaps the most important question of all: is it plausible that the data are Poisson-distributed in the first place?

We last looked at the idea of performing hypothesis tests regarding distributions in Chapter 2, where we introduce the Kolmogorov-Smirnov test for use with arbitrary distributions and the Shapiro-Wilk test to assess the plausibility that our data are normally distributed. So it would seem that here we should work with the KS test, as the Poisson distribution is not the normal distribution…but we can only use the KS test in the context of continuous distributions. So we need a new method!

We can utilize the chi-square goodness-of-fit test. Let’s assume \(\lambda = 0.61\). Then the probabilities \(P(X=x)\) are as follows:

x	P(X=x)	\(E_x\)	\(O_x\)
0	0.543	108.67	109
1	0.331	66.29	65
2	0.101	20.29	22
3	0.021	4.11	3
4	0.003	0.63	1

The conventional rule-of-thumb is that the expected number of counts in each bin must be \(\geq 5\). Here, we will break that rule slightly by combining bins 3 and 4 into one bin with expected counts 4.11 + 0.63 = 4.74. The chi-square GOF test statistic is thus \[ W = \frac{(109-108.67)^2}{108.67} + \frac{(65-66.29)^2}{66.29} + \frac{(22-20.29)^2}{20.29} + \frac{(4-4.74)^2}{4.74} = 0.298 \,. \] This figure can be found using R:

e    <- 200*dpois(0:4,0.61)
e[4] <- e[4]+e[5]
e    <- e[-5]
o    <- c(109,65,22,4)

(W = sum((o-e)^2/e))

## [1] 0.2980418

When using the chi-square GOF test to assess the viability of a distribution whose parameters are estimated, we lose additional degrees of freedom, so the number of degrees of freedom here is 4 - 2 = 2. The \(p\)-value is

1 - pchisq(W,2)

## [1] 0.8615511

We find that we fail to reject the null hypothesis and thus that it is plausible that Bortkiewicz’s horse-kick data are indeed Poisson-distributed.